以下の私的まとめです。
あるデータが得られたときに、そのデータは偶然によるものなのか、偶然以外のものによるものなのか、どちらか判断するときに、仮説検定という手法を用います。
仮説検定(かせつけんてい、英: hypothesis testing)あるいは統計的仮説検定(statistical hypothesis testing)[補 1]とは、母集団分布の母数に関する仮説を標本から検証する統計学的方法のひとつ
出典: フリー百科事典『ウィキペディア(Wikipedia)』
仮説を立てる
帰無仮説 The null hypothesis
端的に言えば、帰無仮説とは、完全にシミュレートできる確率モデルに従ってランダムにデータを選ぶことで、データが生成されたという仮説です。
確率に従ってこういう結果になったのであって、他に特別な要因はありませんという仮説です。
対立仮説 The alternative hypothesis
データを生成した確率モデル以外に、何らかの特別な要因があるとする仮説です。
具体例
コインの裏表で考えると、まずは、「このコインは、裏表、偏りのないコインである」を帰無仮説、「このコインは、裏表、偏りのあるコインである」を対立仮説とするのが妥当です。
もし最初から歪んているのが分かっていて、どの程度歪んでいるかを確認する場合は、表0.6裏0.4というような確率モデルを使って帰無仮説を設定します。
検定統計量を決める The Test Statistic
帰無仮説と対立仮説のどちらかを選ぶために使う統計量を、検定統計量と呼びます。
検定統計量は、帰無仮説、対立仮説、双方から得ることができるものでなければなりません。
検定統計量は、対立仮説を見ながら、どのような統計量があれば対立仮説は帰無仮説より良いと判断できるかという観点から考えます。
「大きい値」で判断できる場合は、良い検定統計量です。
「小さい値」で判断できる場合も、良い検定統計量です。
しかし、「大きい値、小さい値どちらでも」判断できる場合は、検定統計量を考え直す必要があります。
検定統計量の観察された値 The observed value of the test statistic
帰無仮説に基づくシミュレーションではなく、実際の観察により取得した値のことです。
具体例
検定統計量は、「裏と表の回数の差の絶対値」とします。
コインに偏りがあるかを確認するために、100回コインを投げたとします。
実験の結果が表35回裏65回でした。
この場合、検定統計量の観察された値は、30になります。
帰無仮説の下でシミュレート
帰無仮説が正しいと仮定して、検定統計量をシミュレートすることで、 検定統計量の経験分布( empirical distribution )を作り、検定統計量の確率分布を概算します。
具体例
コインを100回投げて、表の裏の回数の差の絶対値を求める作業を、下記のコードで10000回シミュレートします。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
flip_coin = np.array(['head', 'tail'])
array_diffs = np.array([])
for _ in np.arange(10000):
array_flip_coin = np.array([])
for _ in np.arange(100):
flipped_coin = np.random.choice(flip_coin)
array_flip_coin = np.append(array_flip_coin, flipped_coin)
heads = np.count_nonzero(array_flip_coin=='head')
tails = np.count_nonzero(array_flip_coin=='tail')
diff = abs(heads - tails)
array_diffs = np.append(array_diffs, diff)
s = pd.Series(array_diffs)
print((s>=20).sum()/10000 * 100)
print((s>=22).sum()/10000 * 100)
print((s>=30).sum()/10000 * 100)
# s_count = s.value_counts()
plt.hist(s, bins=20)
plt.plot(30,0, marker='.', color='red', markersize=10)
plt.show()
差の絶対値の経験分布( empirical distribution )は、以下のようになりました。
30は赤い点としてプロットしてあります。
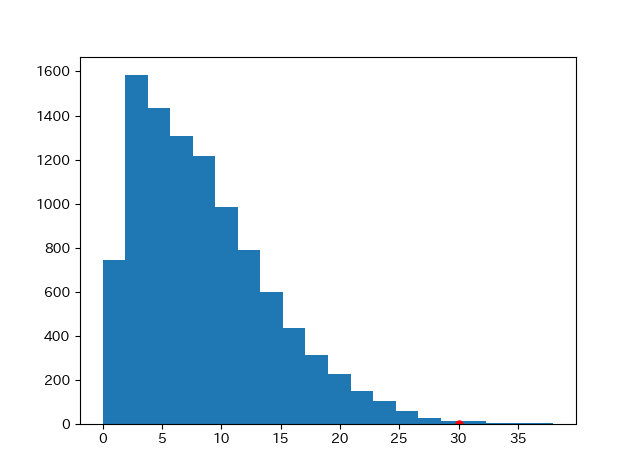
結論
明らかにコインには偏りがあります。
一応P値を求めます。
P値 P-value
帰無仮説の下で、検定統計量が、検定統計量の観察された値か、またはより対立仮説を支持する方向になる確率です。
P値が小さければ小さいほど、帰無仮説は正しくないと考えることができます。
具体例
上のコインのシミュレーションの場合は、P値は、0.3%から0.4%ぐらいになるようです。
これは、帰無仮説が正しい、つまりコインの裏表に偏りは無いとすると、100回投げて表と裏の差が30になる確率は、0.3%から0.4%程度になるということを意味します。
偶然0.3%から0.4%を引くというのは考えにくいことなので、一般的には、コインは偏りがあると考えて良いと思います。
ただし、 偶然0.3%から0.4%を引くということは起こるので、偶然今回の実験ではこのような結果になったと考えることもできないわけではありません。
そこで有意水準というものを使います。
慣習的な有意水準 Conventional P-value Cut-offs
P値があり得そうかどうかという判断基準を有意水準と言い、「P値がこの値より小さければ帰無仮説を否定する基準」とし、帰無仮説が否定された場合は、「統計的に有意である」と表現します。
有意水準自体は、個人がその求めたい確実度合いにより決めて良いものですが、慣習的に1%や5%という値が使われることが多いそうです。
具体例
コインの例では、P値は0.3%から0.4%程度なので、1%水準でも5%水準でも、帰無仮説(コインは偏りはない)は否定され、統計的に有意であると表現されます。
逆に言えば、「帰無仮説(コインが偏りが無い場合)の下では、このようなこと(表と裏の差が30回)は偶然に起こりそうもないが、ごく小さい確率0.3%から0.4%程で起こり得る」 ということを意味しています。
ちなみに、差が20回であればp値は5.5%ぐらい、差が22回であればp値は3.5%ぐらいと、このあたりが5%水準の境目になるようです。