[Python] 現代ポートフォリオ理論

Python で現代ポートフォリオ理論に基づいた最適な資産配分を計算します。

現代ポートフォリオ理論 効率的フロンティア

現代ポートフォリオ理論の効率的フロンティアについて理解します。 wikipedia の内容を、自分レベルでも理解できるようにかみ砕いていきます。 現代ポートフォリオ理論 現代ポートフォリオ理論(げんだいポートフォリオりろん、英:Modern portf...

yottagin.com

2020-03-16 16:29

シャープレシオと効率的フロンティア

以下の理解が前提となります。 シャープレシオ シャープ・レシオ(英:Sharpe ratio)とは投資の効率性を測る指標。1966年にウィリアム・シャープにより提案された。 出典: フリー百科事典『ウィキペディア（Wikipedia）』 ...

yottagin.com

2020-03-17 11:44

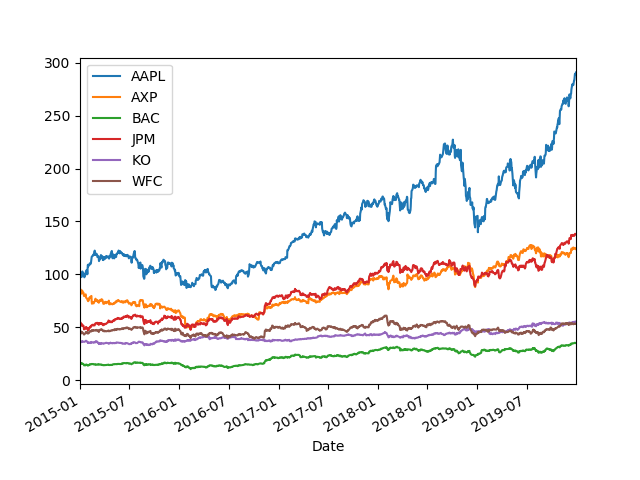
バークシャーハサウェイの2020年2月ポートフォリオ上位6銘柄を使います。

バークシャーハサウェイ（BRK）の最新ポートフォリオ　銀行株売られる

クラフトハインツは合併して間もなくデータが揃わなかったので使わず、JPモルガンを入れました。

株価情報の取得と確認

yfinance を使い株価を取得します。

[Python] アメリカ株の情報取得

株の分析をしてみたくなったのでまとめていきます。 情報の取得が簡単に行えるアメリカ株を対象にします。 モジュール numpy scipy pandas matplotlib は使うとして、他に下記の2つのモジュールを使っていきます。 yfinance ...

yottagin.com

2020-03-12 16:51

何度もデータをダウンロードするのは無駄なのでキャッシュを使います。

Caching queries

収益には日次リターン使うことにします。

また、日次リターンが現代ポートフォリオ理論の前提である正規分布になっているか確認をします。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

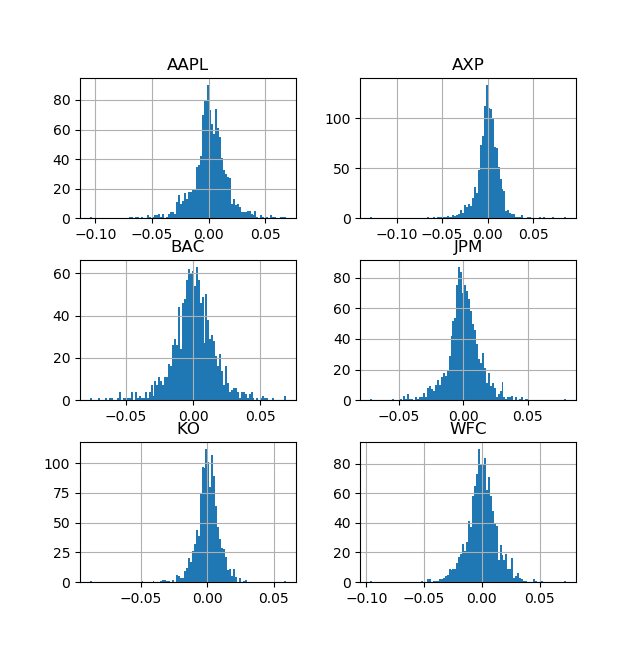
日次リターンの平均と共分散に252をかけることで、年次リターンの平均と共分散を確認します。

How Many Trading Days in a Year?

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

    print(returns.mean()*252)
    print(returns.cov()*252)

AAPL    0.211673
AXP     0.073712
BAC     0.152252
JPM     0.187018
KO      0.086669
WFC     0.026449
dtype: float64
          AAPL       AXP       BAC       JPM        KO       WFC
AAPL  0.061904  0.018407  0.025670  0.022593  0.008349  0.018950
AXP   0.018407  0.042761  0.030271  0.025552  0.008001  0.023154
BAC   0.025670  0.030271  0.066200  0.048190  0.006989  0.042333
JPM   0.022593  0.025552  0.048190  0.044040  0.008305  0.035165
KO    0.008349  0.008001  0.006989  0.008305  0.020189  0.007601
WFC   0.018950  0.023154  0.042333  0.035165  0.007601  0.044489

株式の所持割合

それぞれの株式の所持割合\(w_i\)をランダムに決めます。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns

def initialize_weights(stocks):
    np.random.seed(seed=0)
    weights = np.random.random(len(stocks))
    weights /= np.sum(weights)
    return weights


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

    # print(returns.mean()*252)
    # print(returns.cov()*252)

    weights = initialize_weights(STOCKS)
    # [0.15765074 0.20544344 0.17314824 0.15652173 0.12169798 0.18553787]
    print(weights)

ポートフォリオの期待収益とリスク

Python, NumPyで行列の演算（逆行列、行列式、固有値など）

与えられた所持割合の下でポートフォリオの期待収益を\( {\boldsymbol{ w }}^{ \mathrm{ T }} {\boldsymbol{ \mu} } \)で求めます。

また、ポートフォリオの分散を\( {\boldsymbol{ w }}^{ \mathrm{ T }} {\boldsymbol{ \Omega} \boldsymbol{ w } } \) で求め、標準偏差に変換します。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')
YEARLY_TRAIDING_DAYS = 252

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns

def initialize_weights(stocks):
    np.random.seed(seed=0)
    weights = np.random.random(len(stocks))
    weights /= np.sum(weights)
    return weights

def calc_portfolio_return(returns, weights):
    portfolio_return = np.sum(returns.mean()*weights) * YEARLY_TRAIDING_DAYS
    return portfolio_return

def calc_portfolio_std(returns, weights):
    portfolio_variance = np.dot(weights.T, np.dot((returns.cov()*YEARLY_TRAIDING_DAYS), weights))
    portfolio_standart_deviation = np.sqrt(portfolio_variance)
    return portfolio_standart_deviation


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

    # print(returns.mean()*252)
    # print(returns.cov()*252)

    weights = initialize_weights(STOCKS)
    # # [0.15765074 0.20544344 0.17314824 0.15652173 0.12169798 0.18553787]
    # print(weights)
    
    # 0.11960336203493101
    print(calc_portfolio_return(returns, weights))
    # 0.16633104722051742
    print(calc_portfolio_std(returns, weights))

ポートフォリオのシミュレーション

モンテカルロ法を用いて、ポートフォリオのシミュレーションを行います。

モンテカルロ法

モンテカルロ法 (モンテカルロほう、英: Monte Carlo method, MC) とはシミュレーションや数値計算を乱数を用いて行う手法の総称。

出典: フリー百科事典『ウィキペディア（Wikipedia）』

モンテカルロ法は以下のように行われます。

1. 入力される値のレンジを決める。
2. レンジ内で入力値をランダムに発生させる。
3. ランダムな入力値に基づき数値計算を行う。
4. 1-3を繰り返し結果をまとめる。

モンテカルロ法の例として、円周率の計算が良く使われます。

モンテカルロ法と円周率の近似計算

モンテカルロ法のポートフォリオへの適用

ポートフォリオの重みをランダムに変更し、ポートフォリオのシミュレーションを行い、リスクリターン平面で図示します。

initialize_weights はシードが固定されないように変更します。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')
YEARLY_TRAIDING_DAYS = 252

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns

def initialize_weights(stocks, fixed_seed=False):
    if fixed_seed:
        np.random.seed(0)
    weights = np.random.random(len(stocks))
    weights /= np.sum(weights)
    return weights

def calc_portfolio_return(returns, weights):
    portfolio_return = np.sum(returns.mean()*weights) * YEARLY_TRAIDING_DAYS
    return portfolio_return

def calc_portfolio_std(returns, weights):
    portfolio_variance = np.dot(weights.T, np.dot((returns.cov()*YEARLY_TRAIDING_DAYS), weights))
    portfolio_standart_deviation = np.sqrt(portfolio_variance)
    return portfolio_standart_deviation

def generate_portfolios(returns, stocks):
    p_returns = []
    p_stds = []

    for _ in range(10000):
        weights = initialize_weights(stocks)
        p_returns.append(calc_portfolio_return(returns, weights))
        p_stds.append(calc_portfolio_std(returns, weights))

    return np.array(p_returns), np.array(p_stds)


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

    # print(returns.mean()*252)
    # print(returns.cov()*252)

    # weights = initialize_weights(STOCKS, fixed_seed=True)
    # # [0.15765074 0.20544344 0.17314824 0.15652173 0.12169798 0.18553787]
    # print(weights)
    
    # # 0.11960336203493101
    # print(calc_portfolio_return(returns, weights))
    # # 0.16633104722051742
    # print(calc_portfolio_std(returns, weights))

    p_returns, p_stds = generate_portfolios(returns, STOCKS)
    plt.scatter(p_stds, p_returns, c=p_returns/p_stds)
    plt.grid(True)
    plt.xlabel('Expected Risk')
    plt.ylabel('Expedted Return')
    plt.colorbar(label='Risk-Return-Ratio')
    plt.show()

現代ポートフォリオ理論の理論的なリスクリターン平面と同じような結果を得ることができています。

接点ポートフォリオを求める

安全資産の金利が0の時の接点ポートフォリオを、scipy.optimize.minimize を使い求めます。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# sort for adjsuting stocks to df.colnames 
STOCKS = sorted(['AAPL', 'BAC', 'KO', 'AXP', 'WFC', 'JPM'])
START = pd.to_datetime('2015-01-01') 
END = pd.to_datetime('2019-12-31')
YEARLY_TRAIDING_DAYS = 252

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_daily_returns(data):
    returns = np.log(data/data.shift(1))
    return returns

def initialize_weights(stocks, fixed_seed=False):
    if fixed_seed:
        np.random.seed(0)
    weights = np.random.random(len(stocks))
    weights /= np.sum(weights)
    return weights

def calc_portfolio_return(returns, weights):
    portfolio_return = np.sum(returns.mean()*weights) * YEARLY_TRAIDING_DAYS
    return portfolio_return

def calc_portfolio_std(returns, weights):
    portfolio_variance = np.dot(weights.T, np.dot((returns.cov()*YEARLY_TRAIDING_DAYS), weights))
    portfolio_standart_deviation = np.sqrt(portfolio_variance)
    return portfolio_standart_deviation

def generate_portfolios(returns, stocks):
    p_returns = []
    p_stds = []

    for _ in range(10000):
        weights = initialize_weights(stocks)
        p_returns.append(calc_portfolio_return(returns, weights))
        p_stds.append(calc_portfolio_std(returns, weights))

    return np.array(p_returns), np.array(p_stds)

def statistics(weights, returns):  
    p_return = calc_portfolio_return(returns, weights)
    p_std = calc_portfolio_std(returns, weights)
    return np.array([p_return, p_std, p_return/p_std])

def min_func(weights, returns):
    # p_return/p_std を最大化する
    # つまり -1 * p_return/p_std を最小化する
    return -statistics(weights, returns)[2]

def optimize_portfolio(weights, returns):
    # 0 <= weight_i <= 1
    bounds = tuple((0, 1) for x in range(len(STOCKS)))
    # sum of weights = 1
    constraints = ({'type':'eq', 'fun': lambda x: np.sum(x)-1})
    optimized = scipy.optimize.minimize(
        fun=min_func,
        x0=weights, 
        args=returns,
        method='SLSQP',
        bounds=bounds,
        constraints=constraints,
    )

    return optimized


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(head.head())
    # print(data.tail())
    # # plot data
    # data.plot()
    # plt.show()
    
    returns = calc_daily_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # histgram daily return
    # returns.hist(bins=100)
    # plt.show()

    # print(returns.mean()*252)
    # print(returns.cov()*252)

    # weights = initialize_weights(STOCKS, fixed_seed=True)
    # # [0.15765074 0.20544344 0.17314824 0.15652173 0.12169798 0.18553787]
    # print(weights)
    
    # # 0.11960336203493101
    # print(calc_portfolio_return(returns, weights))
    # # 0.16633104722051742
    # print(calc_portfolio_std(returns, weights))

    p_returns, p_stds = generate_portfolios(returns, STOCKS)
    # plt.scatter(p_stds, p_returns, c=p_returns/p_stds)
    # plt.grid(True)
    # plt.xlabel('Expected Risk')
    # plt.ylabel('Expedted Return')
    # plt.colorbar(label='Risk-Return-Ratio')
    # plt.show()

    weights = initialize_weights(STOCKS, fixed_seed=True)
    optimized = optimize_portfolio(weights, returns)
    optimized_vars = statistics(optimized['x'], returns)
    # optimized weights [0.2959 0.     0.     0.3825 0.3216 0.    ]

    print('optimized weights', optimized['x'].round(4))
    # Expected retrun, risk, SharpeRatio [0.16203813 0.15065529 1.0755555 ]
    print('Expected retrun, risk, SharpeRatio', 
           optimized_vars)

    plt.scatter(p_stds, p_returns, c=p_returns/p_stds)
    plt.grid(True)
    plt.xlabel('Expected Risk')
    plt.ylabel('Expedted Return')
    plt.colorbar(label='Sharpe-Ratio')
    plt.plot(optimized_vars[1], optimized_vars[0], '*r')
    plt.show()

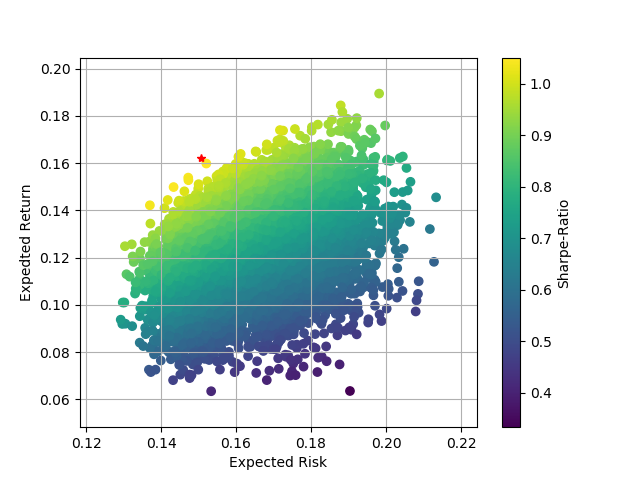
赤色の星形が接点ポートフォリオになります。