二分探索木
二分探索木(にぶんたんさくぎ、英: binary search tree)は、コンピュータプログラムにおいて、「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」という制約を持つ二分木である。探索木のうちで最も基本的な木構造である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
配列と連結リストの計算量を簡単にまとめます。
| 配列 | 連結リスト |
|---|---|
| 要素の挿入 \( O(N)\) | 要素の挿入 \( O(1)\) |
| 2分探索による要素の探索 \( O( \log N)\) | 要素の探索 \( O(N)\) |
| 要素の削除 \( O(N)\) | 要素の削除 \( O(1)\) |
双方のデータ構造とも一長一短で、どの操作を良く使うかによって、使うべきデータ構造を選びます。
しかし、事前にどの操作を良く使うのかわかない場合、またどの操作も同じ程度に使うので、計算量がより折衷的なデータ構造を使いたいという場合、上述の操作を全て\(O (\log N) \) で行うことのできる2分探索木というデータ構造を選ぶことができます。
木構造 Tree
2分探索木は、木構造の一種です。
木構造(きこうぞう)とは、グラフ理論の木の構造をしたデータ構造のこと。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
数学、特にグラフ理論の分野における木(き、英: tree)とは、連結で閉路を持たない(無向)グラフである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
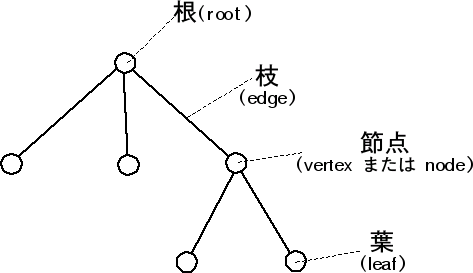
木構造は、データをもつノード(node)とノード間を結ぶエッジ(edge)から成り立ちます。
ルート(root node)と呼ばれるノードがあり、木構造の中のすべてのノードはルートからアクセスできます。またルートからある一つのノードへのアクセスの経路(path)は、必ず一つだけになります。
また、木は高さを持ち、ルートの高さを「0」にして、ルートから一番遠いノードまでのエッジの個数が木の高さになります。
2分探索木の構造
全てのノードは0個、1個、2個のいずれかの子ノードを持っていて、左側の子ノードは親の値より小さい値、右の側の子ノードは親の値より大きい値を持ちます。
結果として 「左の子孫の値 ≤ 親 ≤ 右の子孫の値」 という構造になります。
このような構造を持つことで、それぞれのインデックスはソートされている状態になるので、2分探索と同じように、値を探す際に常に半分ずつ絞っていくことで、計算量は \( O (\log N) \) になります。
これは、木の高さが \( O (\log N) \) になるので、 \( O (\log N) \) の探索で一番遠いノードまでたどりつけることと同じ意味です。
ただし、 \( O (\log N) \) になるのは、木がバランスよく平衡している場合で、もしルートから木が一方向にのみ伸びているような極端な場合は、木の高さは\( O (N) \)になり、 計算量は \( O (N) \) になってしまいます。
よって、木を常にバランス良く平衡させる平衡二分探索木というデータ構造が、2分探索木の発展形として出てきます。
平衡二分探索木(へいこうにぶんたんさくぎ、英: self-balancing binary search tree)とは、計算機科学において二分探索木のうち木の高さ(根からの階層の数)を自動的にできるだけ小さく維持しようとするもの(平衡木)である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
2分探索木の操作
値の挿入・探索
2分探索木の値の挿入は、ルートより値が小さければ左のノードへ、ルートより値が大きければ右のノードへ進み…を繰り返して、次のノードが見つからない場合は、その場所へデータを挿入します。
同様に値の探査も、 ルートより値が小さければ左のノードへ、ルートより値が大きければ右のノードへ進み…を値が見つかるまで繰り返し、もし 次のノードが見つからない場合は、その値は存在しないということになります。
計算量は木の高さに依存して、平衡している木であれば \( O (\log N) \) になります。
最小のノードを探す場合は、左側に進み続けてたどり着くノードが最小のノードに、最大のノードを探す場合は、右側に進み続ければたどり着けます。
2分探索木は、ソート済みの配列で2分探索を行うようなイメージで操作できます。
値の削除
値の削除は、「値が葉である(子供を持たない)場合」「子供が一つの場合」「子供が二つの場合」に分かれます。
葉である(子どもを持たない)場合
値を持つノードを探索して、そのノードを削除するだけです。
探索 \( O (\log N) \) と削除\( O(1) \)で \( O (\log N) \) の計算量になります。
子供が一つの場合
値を持つノードを探索して、そのノードを削除し、削除ノードの親ノードから削除ノードの子ノードへとポインタの付け替えを行います。
探索 \( O (\log N) \) と削除\( O(1) \)と ポインタの付け替え\( O(1) \) で \ \( O (\log N) \) の計算量になります。
子供が二つの場合
値を持つノードを探索します。
その後「削除ノードの左側の部分木で最大のノード」かまたは「削除ノードの右側の部分木で最小のノード」のいずれかを探し、この見つかったノードが削除ノードの場所に入るようポインタの付け替えを行います。
削除のノードの探索と入れ替えノードの探索が \( O (\log N) \) 、その他の操作は \( O(1) \) で \( O (\log N) \) の計算量になります。
2分探索木の走査 traversal
in-order 間順・中間順・通りがけ順
in-order traversal は、「左側の部分木」→「ルート」→「右側の部分木」という順序で再帰的に木を巡ります。
下の図で考えると、■からスタートして、●にあたるところでノードが記録されます。
結果として、ソート順で走査できます。
pre-order 前順・先行順・前置順・行きがけ順
「ルート」→ 「左側の部分木」→「右側の部分木」という順序で再帰的に木を巡ります。
post-order 後順・後行順・後置順・帰りがけ順
「左側の部分木」→「右側の部分木」→ 「ルート」 という順序で再帰的に木を巡ります。
2分探索木の計算量
2分探索木の基本的な操作の計算量は以下のようになります。
| 平均 average case | 最悪 worst case | |
|---|---|---|
| 空間計算量 | \( O (N) \) | \( O (N) \) |
| 挿入 | \( O (\log N) \) | \( O (N) \) |
| 探索 | \( O (\log N) \) | \( O (N) \) |
| 削除 | \( O (\log N) \) | \( O (N) \) |
木が平衡していないと計算量は悪くなってしまいます。