最短経路問題
グラフ理論における最短経路問題(さいたんけいろもんだい、英: shortest path problem)とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
最小経路問題とは、グラフの中でエッジの重みの総和が最小となるような2点間の経路を探す問題です。
例えば、以下のグラフを考えます。
このグラフの「A」から「F」への最短経路は、(A, C, E, D, F) になります。
有名なアルゴリズムとして、ダイクストラ法、 ベルマンフォード法 、ワーシャルフロイド法、A*などがあります。
ダイクストラ法
ダイクストラ法(だいくすとらほう、英: Dijkstra’s algorithm)はグラフ理論における辺の重みが非負数の場合の単一始点最短経路問題を解くための最良優先探索によるアルゴリズムである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ダイクストラ法は、辺の重みが非負数の時に最短経路問題を解くアルゴリズムです。負数の時にはベルマンフォード法を使います。
計算量は、オリジナルでは \( O ( V^2)\)ですが 、2分ヒープの優先度付きキューを使うと\( O ( ( E +V) \times \log V)\)、フィボナッチヒープの優先度付きキューを使うと \( O ( E + V \times \log V)\) と小さくなります。
ダイクストラ法は、貪欲法を基本戦略とするアルゴリズムですが、貪欲法で求まる解が最適解であると帰納法で証明されます。
貪欲法で最適解になる、つまり常に隣接リストの中で最小の距離を持つノードを選んでいけば良いので、minヒープを隣接リストに用いるとで最小距離のノードの選択の計算量を小さくすることができます。
ダイクストラ法は、scipyに含まれており、手軽に利用できます。
ここでは、学習のため自分で実装します。
疑似コード
ダイクストラ法の疑似コードは以下のようになります。
function dijkstra(Graph, start)
# 初期化
# Q は min heap を使ったキュー
create vertex priority_queue Q
# 距離を無限大、前のノードは無し
for v in Graph
distance[v] = inf
predecessor[v] = None
add v to Q
# スタート地点の距離は0
distance[start] = 0
# 計算
while Q not empty
# 最小距離の取得にはヒープを使い計算量を減らす
u = vertex in Q with min distance
remove u from Q
# スタート地点から u までの距離と 、u から v の距離の和
# 現時点でのスタート地点から v までの距離
# 比較して、小さい方をスタート地点から v までの距離に更新
for each reighbor v of u
temp_dist = distance[u] + distance_between(u, v)
if temp_dist < distance[v]
distance[v] = temp_dist
predecessor[v] = u
まず、min ヒープをを使ったキューを用意します。スタート地点の距離は0、その他全てのノードの距離を無限大にしてキューに入れます。
その後、キューから距離が最小となっているノード u を取り出し、取り出したノード u とその隣接するノード v に対して、「隣接ノード v の現時点でのスタート地点からの距離 disitance[v]」と「スタート地点からノード u を経由してノード v に到達する距離 distance[u] + distance_between(u, v)」の比較を行い、小さい方の距離をノード v の距離として更新していきます。この処理を、キューからノードが無くなるまで繰り返します。
最終的に、全てのノードの距離はスタート地点からの最小距離に更新されます。
Python で実装
モジュールのインポート
sys は sys.maxsize を無限大の値として使うためインポートします。
heapq は minheap を使うためにインポートします。
heapq --- ヒープキューアルゴリズム
import sys import heapq
ノード
adjacency_list には、(ノード, 2ノード間の距離)をタプルで格納 することにします。
predecessor は、最短経路を表示する時に、ゴールから開始地点までの経路をたどるために使います。
特殊メソッド__lt__は、ヒープ内でノードの大小比較を距離で行うために定義します。
import sys
import heapq
class Node(object):
def __init__(self, name):
self.name = name
# adjacency_list には(ノード, 2ノード間の距離)を格納
self.adjacency_list = []
self.min_distance = sys.maxsize
self.visited = False
self.predecessor = None
# heapq を使うために必要。
# heapq 内での大小関係を min_distance に基づいて処理する。
def __lt__(self, other_vertex):
return self.min_distance < other_vertex.min_distance
最短距離の計算
calculate_shortest_path は、疑似コードとほぼ同じです。
ヒープキューは、最初に全てのノードをヒープキューに入れるのではなく、幅優先探索のような感じで隣接リストにあるノードをキューに入れるように処理をしています。
show_shortest_path は、 culate_shortest_path の結果を使い、目的のノードまでの最短経路と最短距離を表示します。経路の取得は、 predecessor をバックトラックすることで行います。
import sys
import heapq
class Node(object):
def __init__(self, name):
self.name = name
# adjacency_list には(ノード, 2ノード間の距離)を格納
self.adjacency_list = []
self.min_distance = sys.maxsize
self.visited = False
self.predecessor = None
# heapq を使うために必要。
# heapq 内での大小関係を min_distance に基づいて処理する。
def __lt__(self, other_vertex):
return self.min_distance < other_vertex.min_distance
class Dijkstra(object):
def __init__(self, start_node):
self.start_node = start_node
def calculate_shortest_path(self):
q = []
self.start_node.min_distance = 0
heapq.heappush(q, self.start_node)
while q:
current_node = heapq.heappop(q)
current_node.visited = True
for next_node, distance in current_node.adjacency_list:
if not next_node.visited:
temp_dist = current_node.min_distance + distance
if temp_dist < next_node.min_distance:
next_node.min_distance = temp_dist
next_node.predecessor = current_node
heapq.heappush(q, next_node)
def show_shortest_path(self, goal):
current_node = goal
order_list = []
while current_node is not None:
order_list.append(current_node.name)
current_node = current_node.predecessor
print(f'from {self.start_node.name} to {goal.name} distance {goal.min_distance}', order_list[::-1])
テスト
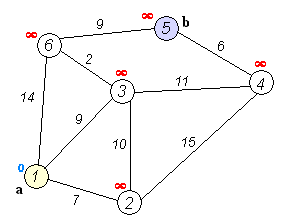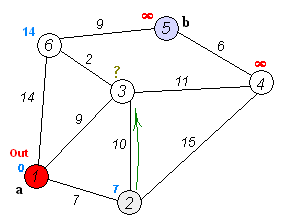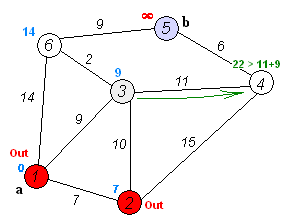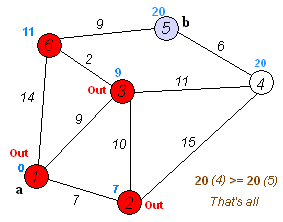
以下のグラフで1からの最短経路を計算します。
import sys
import heapq
class Node(object):
def __init__(self, name):
self.name = name
# adjacency_list には(ノード, 2ノード間の距離)を格納
self.adjacency_list = []
self.min_distance = sys.maxsize
self.visited = False
self.predecessor = None
# heapq を使うために必要。
# heapq 内での大小関係を min_distance に基づいて処理する。
def __lt__(self, other_vertex):
return self.min_distance < other_vertex.min_distance
class Dijkstra(object):
def __init__(self, start_node):
self.start_node = start_node
def calculate_shortest_path(self):
q = []
self.start_node.min_distance = 0
heapq.heappush(q, self.start_node)
while q:
current_node = heapq.heappop(q)
current_node.visited = True
for next_node, distance in current_node.adjacency_list:
if not next_node.visited:
temp_dist = current_node.min_distance + distance
if temp_dist < next_node.min_distance:
next_node.min_distance = temp_dist
next_node.predecessor = current_node
heapq.heappush(q, next_node)
def show_shortest_path(self, goal):
current_node = goal
order_list = []
while current_node is not None:
order_list.append(current_node.name)
current_node = current_node.predecessor
print(f'from {self.start_node.name} to {goal.name} distance {goal.min_distance}', order_list[::-1])
if __name__ == '__main__':
one = Node('one')
two = Node('two')
three = Node('three')
four = Node('four')
five = Node('five')
six = Node('six')
one.adjacency_list.extend([(two, 7), (three, 9), (six, 14)])
two.adjacency_list.extend([(one, 7), (three, 10), (four, 15)])
three.adjacency_list.extend([(one, 9), (two, 10), (four, 11), (six, 2)])
four.adjacency_list.extend([(two, 15), (three, 11), (five, 6)])
five.adjacency_list.extend([(four, 6), (six, 9)])
six.adjacency_list.extend([(one, 14), (three, 2), (five, 9)])
dijkstra = Dijkstra(one)
dijkstra.calculate_shortest_path()
# from one to two distance 7 ['one', 'two']
dijkstra.show_shortest_path(two)
# from one to three distance 9 ['one', 'three']
dijkstra.show_shortest_path(three)
# from one to four distance 20 ['one', 'three', 'four']
dijkstra.show_shortest_path(four)
# from one to five distance 20 ['one', 'three', 'six', 'five']
dijkstra.show_shortest_path(five)
# from one to six distance 11 ['one', 'three', 'six']
dijkstra.show_shortest_path(six)