以前にまとめた赤黒木は以下です。
赤黒木 Red Black Tree
赤黒木(あかくろぎ)は、コンピュータ科学のデータ構造である平衡二分木の一種で、主に連想配列の実装に用いられている。2色木、レッド・ブラック・ツリーともいう。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
2分探索木では最悪の場合\( O (N) \) の計算量になってしまうので、AVL木は、「左右の部分木の高さの差の絶対値を1以下」に保つことで、木を平衡させ計算量を \( O ( \log N) \) にします。
同じように木の平衡を保つ2分木として、赤黒木があります。
AVL木と赤黒木を比較すると、AVL木は赤黒木よりも厳密に平衡を保ち、挿入や削除はの操作は遅くなりますが、検索速度は上がります。
よって、データの追加の少ないデータベースにはAVL木が、データの追加が多い場合には赤黒木が優位になります。
赤黒木の計算量はAVL木と同様になります。
| 平均 average case | 最悪 worst case | |
|---|---|---|
| 空間計算量 | \( O(N) \) | \( O(N) \) |
| 挿入 | \( O(\log N) \) | \( O(\log N) \) |
| 探索 | \( O(\log N) \) | \( O(\log N) \) |
| 削除 | \( O(\log N) \) | \( O(\log N) \) |
Red Black properties 赤黒の特性
AVL木では、全てのノードは高さを保持しましたが、赤黒木は以下のような特性を常に維持し、挿入や削除の操作で特性が守れない場合には、AVL木のように「回転」操作を行います。
- 各ノードは赤か黒の色を持ちます。
- ルートの色は常に黒になります。
- 葉ノード(NILまたは Null) はすべて黒になります。
- 赤ノードは黒ノードを 2つ子に持ちます。つまり、赤のノードの親は常に黒ノードになります。
- 任意のノードについて、そのノードから子孫の葉ノード(NILまたは Null) への経路に含まれる黒ノードの数は、一定になります。(この条件は、「ルートから 葉ノード(NILまたは Null) までの経路に含まれる黒ノードの数は一定である」と言い換えることができます)。
回転と色変更
赤黒木は、「回転」操作や「ノードの色の変更」により “Red Black properties” を維持します。
回転はAVL木の回転と同じ操作で、木の特性を保ったままで木の構成を変更します。ポインタの付け替えを行うだけなので、\( O (1) \) の計算量です。
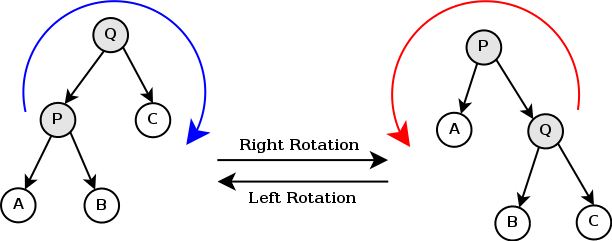
回転を行っても、例えば in-order で取得する要素順や、一番左の子が最小、一番右の子が最大といった木の特性は変わりません。「右回転」「左回転」があり、お互いが逆の操作になります。
色変更は、黒ノードなら赤ノードに、赤ノードなら黒ノードに変更するだけです。
ノードの挿入を行う時、ノードは最初赤色として挿入されます。
2分探索木やAVL木と同じような操作でノードは挿入され、挿入後、”Red Black properties” が守られているか確認します。
もし守られていない場合は、「回転」操作や「ノードの色の変更」により “Red Black properties” を維持します。
木の平衡性が保たれる理由
赤黒木の特性によって、どうして木の平衡性が保たれるのかを考えます。
- 赤ノードは黒ノードを 2つ子に持ちます。つまり、赤のノードの親は常に黒ノードになります。
- 任意のノードについて、そのノードから子孫の葉ノード(NILまたは Null) への経路に含まれる黒ノードの数は、一定になります。(この条件は、「ルートから 葉ノード(NILまたは Null) までの経路に含まれる黒ノードの数は一定である」と言い換えることができます)。
「ルートから 葉ノード(NILまたは Null) までの経路に含まれる黒ノードの数」を\( m\) とします。2)より、全てのルートからの黒ノードの数は \( m\) になります。
1)より、この経路の中で、最短経路は\( m \)個の黒ノードのみからなる経路になります。また、最長経路は「赤」「黒」が交互に現れる経路で \( 2m \)個のノードからなります。
よって、”Red Black properties” を維持する限り、「 根から葉まで道で最長のものの長さ \( 2m \) は、根から葉までの道で最短のものの長さ \( m \) の2倍を超えない」ことになり、赤黒木はある程度の平衡性を保つことができます。
回転・色辺王の場合分け
赤黒木の回転を考える時に、 挿入するノードをN (New Node)、親をP (Parent Node)、叔父をU (Uncle Node)、兄弟をS (Sibling Node)、親の親をG (Grandparent Node) として考える必要があります。
新しく挿入されるノードNは赤色です。
以下のような位置関係になります。
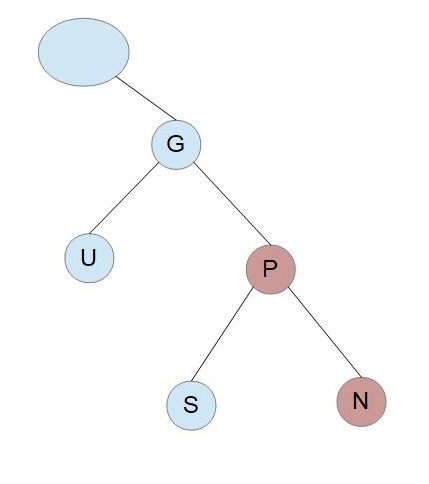
Pが赤でUも赤の場合
Gは必然的に黒になります。
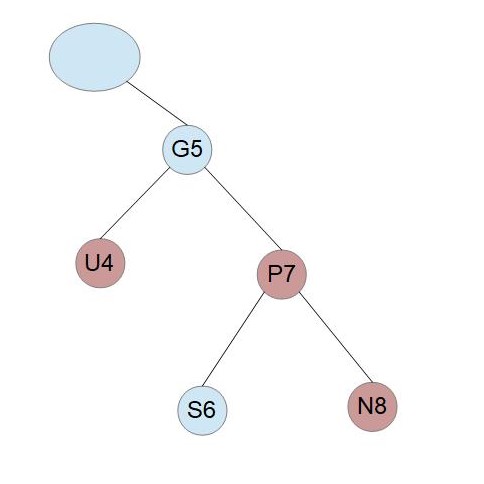
この場合は、G、U、Pの色を反転させます。
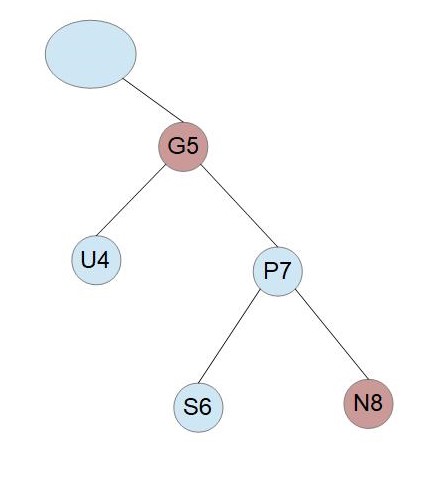
この操作で、この部分木の “Red Black properties” は維持されますが、より上方の部分木に影響を与える可能性があるので、再帰的にルートまで確認が必要です。
Pが赤でUは黒、PはGの左の子、NはPの右の子である場合
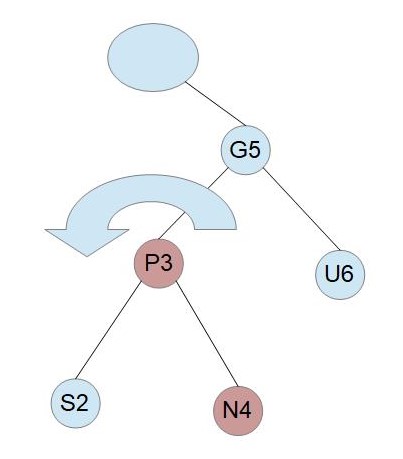
まずは左回転を行います。
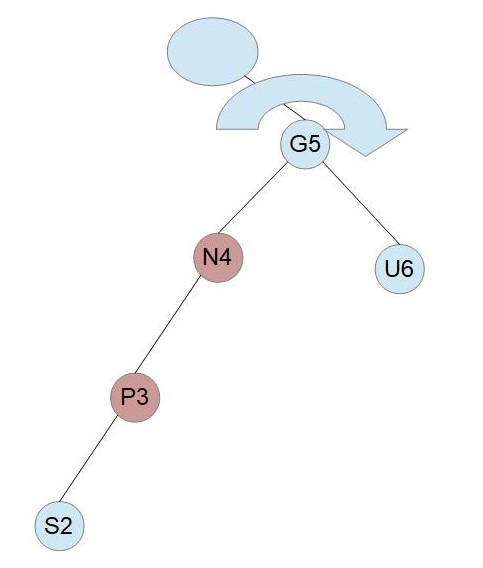
右回転を行います。

N、Gの色を反転します。

「Pが赤でUは黒、PはGの右の子、NはPの左の子」である場合は、上の場合と対称になっています。

Pが赤でUは黒、PはGの左の子、NはPの左の子である場合
このケースは、前述の操作で最初に左回転を行った後と同じ状態になっています。
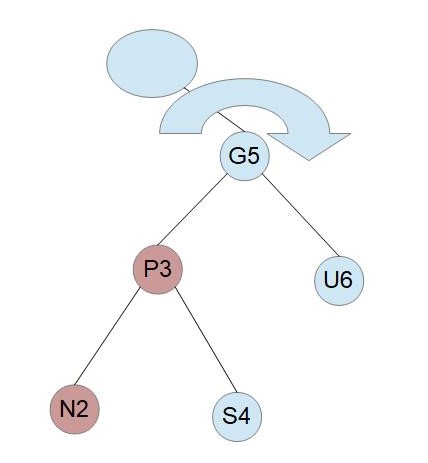
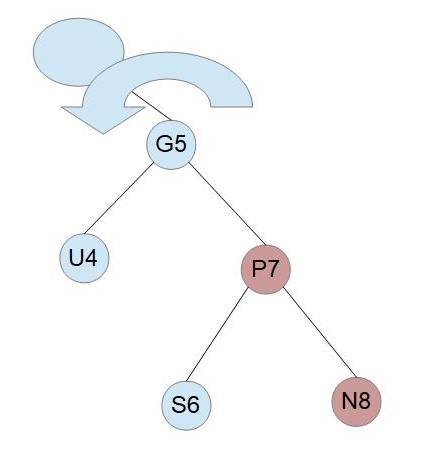
右回転を行います。
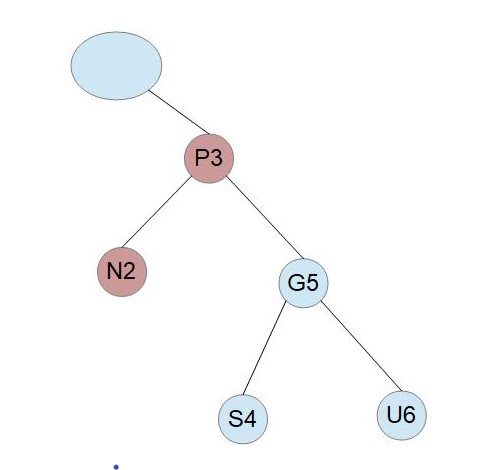
PとGの色を反転します。
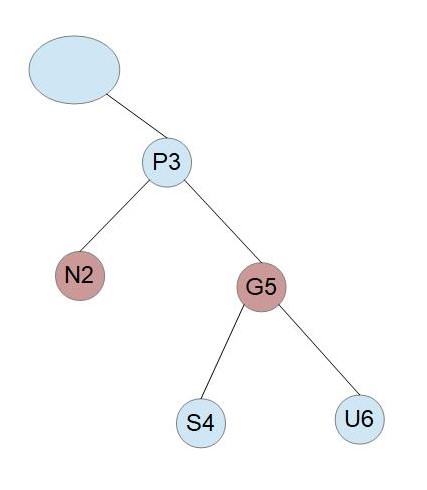
「Pが赤でUは黒、PはGの右の子、NはPの右の子」である場合は、この場合の左右対称なケースになります。
赤黒木とAVL木の比較
赤黒木の平衡性は、根から葉まで道で最長のものの長さ \( 2m \) は、根から葉までの道で最短のものの長さ \( m \) の2倍を超えない」です。
AVL木の平衡性は、「左右の部分木の高さの差が1以下」です。
比較すると、赤黒木の平衡性は、AVL木に比べ緩いです。
よって、 AVL木は赤黒木よりも厳密に木の平衡が保たれるので、検索速度は速くなります。一方で、赤黒木は、 挿入時に木の平衡性をAVL木ほど厳密に保つ必要がないので、データ挿入時の回転操作が少なくて済みます。
よて、データの挿入が多い場合は赤黒木が、データの検索が多い場合はAVL木が向いています。


