問題
音声を標本化周波数10kHz,量子化ビット数16ビットで4秒間サンプリングして音声データを取得した。この音声データを,圧縮率1/4のADPCMを用いて圧縮した場合のデータ量は何kバイトか。ここで,1kバイトは1,000バイトとする。
- 10
- 20
- 80
- 160
答え
20
解説
\( 10k \times 16 \times 4 \)が音声データのビット数になります。
このデータを1/4に圧縮して、さらにバイト( = 8 bit ) に直します。
\( \frac {10k \times 16 \times 4} {4 \times 8 } = 20k\) が答えになります。
標本化周波数(サンプリング周波数)
サンプリング周波数(サンプリングしゅうはすう)は、音声等のアナログ波形を、デジタルデータにするために必要な処理である標本化(サンプリング)で、単位時間あたりに標本を採る頻度。単位はHzが一般に使われるが、sps (sample per second) を使うこともある。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
標本化周波数よりもサンプリング周波数と言われた方が分かりやすい気がします。
音声のアナログ信号からデジタル信号へのA/D変換を行う時に、データをサンプリング(標本化)する時間の間隔が必要になります。
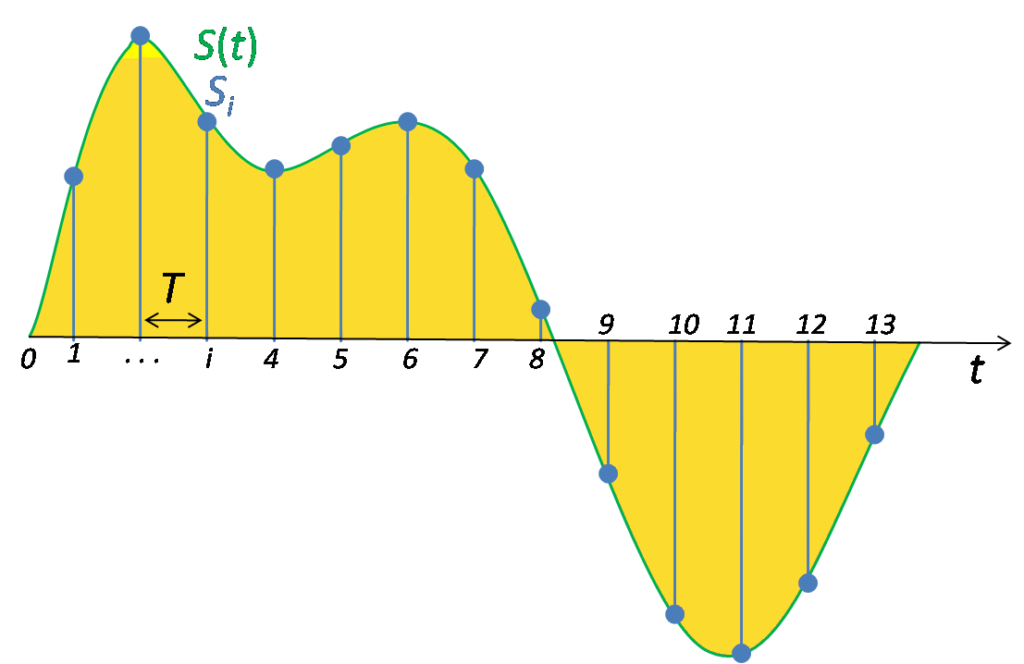
この時、1秒間に何個のサンプルを取得しているかをサンプリング周波数と呼びます。
つまり、標本化周波数(サンプリング周波数)とは、アナログ信号からデジタル信号に変換するために、どのぐらいの時間間隔で区切るかを表します。
問題の標本化周波数10kHzは、10 × 1000 = 10000 回/秒のデータを取得します。
量子化
情報理論や信号処理において、標本化で得られた離散時間信号のようなアナログデータ(連続量)をデジタルデータなどの離散的な値で近似的に表すこと。値をあらわすのに用いるビット数を量子化ビット数と言い、一般に、これを増やして、離散値としてとりうる値の範囲を広げると、量子化誤差が減り、量子化の精度が上がる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
例えば、サンプリングしたデータが、\(\{1, 2, 3, 4\}\)という4つのデータから成り立っていたとします。
1ビットの量子化では、2種類にしか分けることができないので、例えば\(\{1, 2\}\)と\(\{3, 4\}\)と分けます。
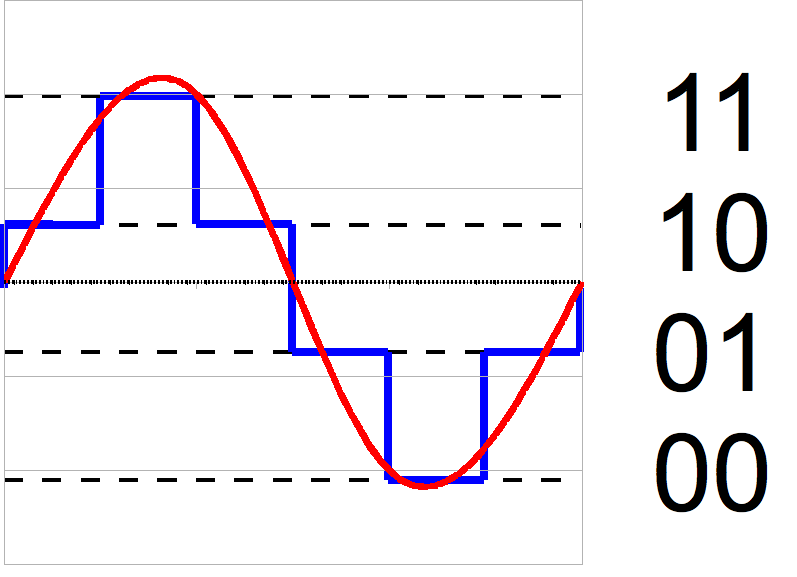
2ビットの量子化では、4種類に分けることができるので、\(\{1\}, \{2\}, \{3\}, \{4\}\)と分けることができ、1ビットの量子化と比較してデータ容量は増えますが精度は上がります。
下の図は、2ビットでの量子化の例で、連続したアナログの値を、4つの数値に量子化しているものです。
問題の量子化ビット数16ビットは、取得したデータを16ビットに分類することを意味します。
パルス符号変調
パルス符号変調とは、パルス(波)を符号(コード)に変換する方式(音波からデジタルデータへの変換を行う方式)のことです。
問題に出てくるADPCMは、ただ単純に変換するより効率の良いパルス符号変調の方式です。
DPCM
差分パルス符号変調(さぶんパルスふごうへんちょう、英: differential pulse-code modulation、DPCM)あるいは差分PCM(英: differential PCM)とは信号間の差分を PCM 符号化する方式である。単純な処理で情報の圧縮ができるため、差分PCMの応用である ADPCM と共に音声符号化や画像符号化の分野で古くから使われている。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
一般的に、隣接サンプルの差をとって得られる信号は,元の音声よりも信号の散らばりの程度を小さくすることができます。 量子化をこのように差分によって行うことを、DPCMと呼びます。
ADPCM
適応的差分パルス符号変調(adaptive differential pulse code modulation:ADPCM、適応的差分PCM あるいは 適応差分PCM)とは自然信号に対する圧縮方式の一つである。主に音声信号に用いられる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
過去の値から現在の値をある程度予測することで、DPCMをさらに圧縮する方法です。