平衡二分探索木
平衡二分探索木（へいこうにぶんたんさくぎ、英:self-balancing binary search tree）とは、計算機科学において二分探索木のうち木の高さ（根からの階層の数）を自動的にできるだけ小さく維持しようとするもの（平衡木...
yottagin.com
2020-01-28 13:03
Python でAVL木を実装します。
ノード
2分探索木とあまり変わりません。
height というインスタンス変数を設定し、ノードの高さを保持します。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
AVL
平衡係数の取得
まずは、ノードの高さを取得する関数 get_height を定義します。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
class AVL(object):
def __init__(self):
self.root = None
def get_height(self, node):
if not node:
return -1
return node.height
def get_balance(self, node):
'''
返り値が1より大きい場合、左の部分木が重い → 右回転
返り値が-1より小さい場合、右の部分木が重い → 左回転
'''
if not node:
return 0
return self.get_height(node.left_child) - self.get_height(node.right_child)
get_heightを使い、左右の部分木の高さの差 （=平衡係数）を取得する関数get_balanceを設定します。
この関数の返り値が1より大きい（平衡係数> 1 ）場合、左の部分木が重いということで、木の平衡を保つため、最終的に右回転を行います。逆に返り値が-1より小さい （平衡係数> ‐1 ） 場合、右の部分木が重いので、最終的に左回転を行います。
回転
右回転を考えます。
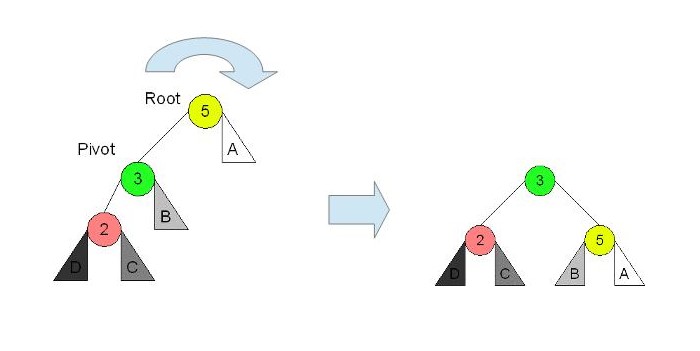
まずは、tempに対象ノードを入れて、子ノードのポインタ付け替えを行います。
元々のルートと左側の子は、それぞれ子ノードが変わり高さが変わっているので、高さの再計算を行います。
最後にルートを再設定するため、新しいルートを返します。
左回転は、これと逆の操作になります。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
class AVL(object):
def __init__(self):
self.root = None
def get_height(self, node):
if not node:
return -1
return node.height
def get_balance(self, node):
'''
返り値が1より大きい場合、左の部分木が重い → 右回転
返り値が-1より小さい場合、右の部分木が重い → 左回転
'''
if not node:
return 0
return self.get_height(node.left_child) - self.get_height(node.right_child)
def rotate_right(self, node):
temp_left_child = node.left_child
temp_left_right_child = temp_left_child.right_child
temp_left_child.right_child = node
node.left_child = temp_left_right_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_left_child.height = max(self.get_height(temp_left_child.left_child), self.get_height(temp_left_child.right_child)) + 1
return temp_left_child
def rotate_left(self, node):
temp_right_child = node.right_child
temp_right_left_child = temp_right_child.left_child
temp_right_child.left_child = node
node.right_child = temp_right_left_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_right_child.height = max(self.get_height(temp_right_child.left_child), self.get_height(temp_right_child.right_child)) + 1
return temp_right_child
挿入
データの挿入を行います。
2分探索と同様に再帰的に処理し、ポインタの付け替えは、_insert の返り値を用いて行います。
ノードの高さの更新を行い、それに応じて木の平衡を保ちます。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
class AVL(object):
def __init__(self):
self.root = None
def get_height(self, node):
if not node:
return -1
return node.height
def get_balance(self, node):
'''
返り値が1より大きい場合、左の部分木が重い → 右回転
返り値が-1より小さい場合、右の部分木が重い → 左回転
'''
if not node:
return 0
return self.get_height(node.left_child) - self.get_height(node.right_child)
def rotate_right(self, node):
temp_left_child = node.left_child
temp_left_right_child = temp_left_child.right_child
temp_left_child.right_child = node
node.left_child = temp_left_right_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_left_child.height = max(self.get_height(temp_left_child.left_child), self.get_height(temp_left_child.right_child)) + 1
return temp_left_child
def rotate_left(self, node):
temp_right_child = node.right_child
temp_right_left_child = temp_right_child.left_child
temp_right_child.left_child = node
node.right_child = temp_right_left_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_right_child.height = max(self.get_height(temp_right_child.left_child), self.get_height(temp_right_child.right_child)) + 1
return temp_right_child
def insert(self, data):
print(f'--------------')
print(f'start inserting {data}')
self.root = self._insert(data, self.root)
print(f'finish inserting {data}')
print(f'--------------')
def _insert(self, data, node):
if not node:
return Node(data)
if data < node.data:
node.left_child = self._insert(data, node.left_child)
else:
node.right_child = self._insert(data, node.right_child)
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
return self.settle_unbalance(data, node)
def settle_unbalance(self, data, node):
balance = self.get_balance(node)
# balace >1 -> 左の方が重い
# data < node.left_child.data 左の子より左側にデータが挿入されたので、左の子の左の子の方が重い
# つまり、left-left heavy 右回転を行う
if balance > 1 and data < node.left_child.data:
print('left-left heavy')
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data > node.right_child.data 右の子より右側にデータが挿入されたので、右の子の右の子の方が重い
# つまり、right-right heavy 左回転を行う
if balance < -1 and data > node.right_child.data:
print('right-right heavy')
return self.rotate_left(node)
# balace >1 -> 左の方が重い
# data > node.left_child.data 左の子より右側にデータが挿入されたので、左の子の右の子の方が重い
# つまり、left-right heavy 左回転を行い右回転を行う
if balance > 1 and data > node.left_child.data:
print('left-right heavy')
node.left_child = self.rotate_left(node.left_child)
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data < node.right_child.data 右の子より左側にデータが挿入されたので、右の子の左の子の方が重い
# つまり、right-left heavy 右回転を行い左回転を行う
if balance < -1 and data < node.right_child.data:
node.right_child = self.rotate_right(node.right_child)
print('right-left heavy')
return self.rotate_left(node)
return node
2分探索木と同様の in-order traversal を使い、挿入が正しく行われているか確認をします。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
class AVL(object):
def __init__(self):
self.root = None
def get_height(self, node):
if not node:
return -1
return node.height
def get_balance(self, node):
'''
返り値が1より大きい場合、左の部分木が重い → 右回転
返り値が-1より小さい場合、右の部分木が重い → 左回転
'''
if not node:
return 0
return self.get_height(node.left_child) - self.get_height(node.right_child)
def rotate_right(self, node):
temp_left_child = node.left_child
temp_left_right_child = temp_left_child.right_child
temp_left_child.right_child = node
node.left_child = temp_left_right_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_left_child.height = max(self.get_height(temp_left_child.left_child), self.get_height(temp_left_child.right_child)) + 1
return temp_left_child
def rotate_left(self, node):
temp_right_child = node.right_child
temp_right_left_child = temp_right_child.left_child
temp_right_child.left_child = node
node.right_child = temp_right_left_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_right_child.height = max(self.get_height(temp_right_child.left_child), self.get_height(temp_right_child.right_child)) + 1
return temp_right_child
def insert(self, data):
print(f'--------------')
print(f'start inserting {data}')
self.root = self._insert(data, self.root)
print(f'finish inserting {data}')
print(f'--------------')
def _insert(self, data, node):
if not node:
return Node(data)
if data < node.data:
node.left_child = self._insert(data, node.left_child)
else:
node.right_child = self._insert(data, node.right_child)
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
return self.settle_unbalance(data, node)
def settle_unbalance(self, data, node):
balance = self.get_balance(node)
# balace >1 -> 左の方が重い
# data < node.left_child.data 左の子より左側にデータが挿入されたので、左の子の左の子の方が重い
# つまり、left-left heavy 右回転を行う
if balance > 1 and data < node.left_child.data:
print('left-left heavy')
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data > node.right_child.data 右の子より右側にデータが挿入されたので、右の子の右の子の方が重い
# つまり、right-right heavy 左回転を行う
if balance < -1 and data > node.right_child.data:
print('right-right heavy')
return self.rotate_left(node)
# balace >1 -> 左の方が重い
# data > node.left_child.data 左の子より右側にデータが挿入されたので、左の子の右の子の方が重い
# つまり、left-right heavy 左回転を行い右回転を行う
if balance > 1 and data > node.left_child.data:
print('left-right heavy')
node.left_child = self.rotate_left(node.left_child)
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data < node.right_child.data 右の子より左側にデータが挿入されたので、右の子の左の子の方が重い
# つまり、right-left heavy 右回転を行い左回転を行う
if balance < -1 and data < node.right_child.data:
node.right_child = self.rotate_right(node.right_child)
print('right-left heavy')
return self.rotate_left(node)
return node
def traverse_inorder(self):
if self.root:
self._traverse_inorder(self.root)
# 改行対策
print()
else:
print('木は空です。')
def _traverse_inorder(self, node):
if node.left_child:
self._traverse_inorder(node.left_child)
print(node.data, end=' ')
if node.right_child:
self._traverse_inorder(node.right_child)
if __name__ == '__main__':
avl = AVL()
avl.insert(2)
avl.insert(4)
# right-right heavy
avl.insert(8)
avl.insert(16)
# right-right heavy
avl.insert(32)
# right-left heavy
avl.insert(14)
# 2 4 8 14 16 32
avl.traverse_inorder()
# height 2
print('height', avl.get_height(avl.root))
avl = AVL()
avl.insert(32)
avl.insert(16)
# left-left heavy
avl.insert(8)
avl.insert(4)
# left-left heavy
avl.insert(2)
# left-right heavy
avl.insert(14)
# 2 4 8 14 16 32
avl.traverse_inorder()
# height 2
print('height', avl.get_height(avl.root))
削除
2分探索木と同様に再帰的にノード削除を行い、その後それぞれのノードの平衡を確認します。
class Node(object):
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
self.height = 0
class AVL(object):
def __init__(self):
self.root = None
def get_height(self, node):
if not node:
return -1
return node.height
def get_balance(self, node):
'''
返り値が1より大きい場合、左の部分木が重い → 右回転
返り値が-1より小さい場合、右の部分木が重い → 左回転
'''
if not node:
return 0
return self.get_height(node.left_child) - self.get_height(node.right_child)
def rotate_right(self, node):
temp_left_child = node.left_child
temp_left_right_child = temp_left_child.right_child
temp_left_child.right_child = node
node.left_child = temp_left_right_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_left_child.height = max(self.get_height(temp_left_child.left_child), self.get_height(temp_left_child.right_child)) + 1
return temp_left_child
def rotate_left(self, node):
temp_right_child = node.right_child
temp_right_left_child = temp_right_child.left_child
temp_right_child.left_child = node
node.right_child = temp_right_left_child
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
temp_right_child.height = max(self.get_height(temp_right_child.left_child), self.get_height(temp_right_child.right_child)) + 1
return temp_right_child
def insert(self, data):
self.root = self._insert(data, self.root)
def _insert(self, data, node):
if not node:
return Node(data)
if data < node.data:
node.left_child = self._insert(data, node.left_child)
else:
node.right_child = self._insert(data, node.right_child)
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
return self.settle_unbalance(data, node)
def settle_unbalance(self, data, node):
balance = self.get_balance(node)
# balace >1 -> 左の方が重い
# data < node.left_child.data 左の子より左側にデータが挿入されたので、左の子の左の子の方が重い
# つまり、left-left heavy 右回転を行う
if balance > 1 and data < node.left_child.data:
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data > node.right_child.data 右の子より右側にデータが挿入されたので、右の子の右の子の方が重い
# つまり、right-right heavy 左回転を行う
if balance < -1 and data > node.right_child.data:
return self.rotate_left(node)
# balace >1 -> 左の方が重い
# data > node.left_child.data 左の子より右側にデータが挿入されたので、左の子の右の子の方が重い
# つまり、left-right heavy 左回転を行い右回転を行う
if balance > 1 and data > node.left_child.data:
node.left_child = self.rotate_left(node.left_child)
return self.rotate_right(node)
# balace > -1 -> 右の方が重い
# data < node.right_child.data 右の子より左側にデータが挿入されたので、右の子の左の子の方が重い
# つまり、right-left heavy 右回転を行い左回転を行う
if balance < -1 and data < node.right_child.data:
node.right_child = self.rotate_right(node.right_child)
return self.rotate_left(node)
return node
def traverse_inorder(self):
if self.root:
self._traverse_inorder(self.root)
# 改行対策
print()
else:
print('木は空です。')
def _traverse_inorder(self, node):
if node.left_child:
self._traverse_inorder(node.left_child)
print(node.data, end=' ')
if node.right_child:
self._traverse_inorder(node.right_child)
def remove(self, data):
if self.root:
self.root = self._remove(data, self.root)
def _remove(self, data, node):
if data < node.data:
node.left_child = self._remove(data, node.left_child)
elif data > node.data:
node.right_child = self._remove(data, node.right_child)
else:
# 削除ノードが子を持たない場合は、ノードを削除する。
if not node.right_child and not node.left_child:
del node
# None を返すことで、親ノードの削除子ノードへのポインタを None に変更
return None
# 削除ノードが左の子だけを持つ場合、ノードを削除し、左の子のノードを返す
if not node.right_child:
temp = node.left_child
del node
# 左の子のノードを返すことで、親ノードの削除子ノードへのポインタを新しい子ノードに変更
return temp
# 削除ノードが右の子だけを持つ場合、左の子だけの場合の逆の操作を行う
if not node.left_child:
temp = node.right_child
del node
return temp
# 削除ノードが左右の子を持つ場合、ここでは、左側のsubtreeの最大のノードを代わりのノードにすることにする。
# subtreeの最大のノードを取得するヘルパー関数
def _get_max_node(node):
if node.right_child:
return _get_max_node(node.right_child)
return node
temp = _get_max_node(node.left_child)
node.data = temp.data
# 左側のsubtreeから削除ノードと入れ替えたノードを削除
node.left_child = self._remove(temp.data, node.left_child)
# 単体の木の場合
if not node:
return node
node.height = max(self.get_height(node.left_child), self.get_height(node.right_child)) + 1
balance = self.get_balance(node)
if balance > 1 and self.get_balance(node.left_child) >= 0:
print('left-left heavy')
return self.rotate_right(node)
if balance < -1 and self.get_balance(node.left_child) <= 0:
print('right-right heavy')
return self.rotate_left(node)
if balance > 1 and self.get_balance(node.left_child) < 0:
print('left-right heavy')
node.left_child = self.rotate_left(node.left_child)
return self.rotate_right(node)
if balance < -1 and self.get_balance(node.left_child) > 0:
node.right_child = self.rotate_right(node.right_child)
print('right-left heavy')
return self.rotate_left(node)
return node
if __name__ == '__main__':
avl = AVL()
avl.insert(2)
avl.insert(4)
avl.insert(8)
avl.insert(16)
avl.insert(32)
avl.insert(64)
avl.insert(128)
avl.insert(256)
avl.insert(512)
# 2 4 8 16 32 64 128 256 512
avl.traverse_inorder()
avl.remove(2)
# right-right heavy
avl.remove(4)
avl.remove(512)
avl.remove(256)
# left-left heavy
avl.remove(128)
avl.remove(64)
# 8 16 32
avl.traverse_inorder()
# height 1
print('height', avl.get_height(avl.root))
以前にまとめた赤黒木は以下です。
赤黒木 Red Black Tree
赤黒木（あかくろぎ）は、コンピュータ科学のデータ構造である平衡二分木の一種で、主に連想配列の実装に用いられている。2色木、レッド・ブラック・ツリーともいう。 出...
yottagin.com
2020-01-30 12:18