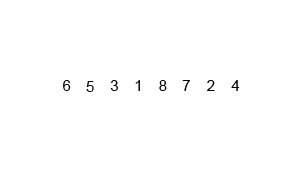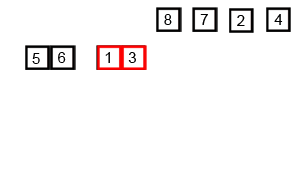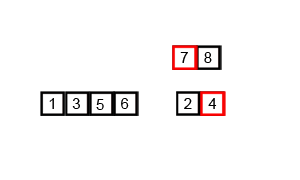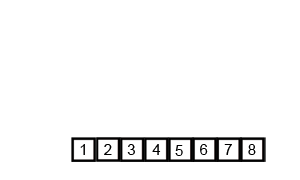[ソート] マージソート

マージソート

マージソートは、ソートのアルゴリズムで、既に整列してある複数個の列を1個の列にマージする際に、小さいものから先に新しい列に並べれば、新しい列も整列されている、というボトムアップの分割統治法による。大きい列を多数の列に分割し、そのそれぞれをマージする作業は並列化できる。
出典: フリー百科事典『ウィキペディア（Wikipedia）』

クイックソートと同じような分割統治法のソートアルゴリズムです。

リストを2つに分割して、分割されたリストに含まれるデータが1個ならそれを返ます。

リストに含まれるデータが2個以上の時は、そのリストにマージソートを再帰的に適用し、その結果として返ってきたソート済みのリストを、ソートしながら一つのリストにまとめます。

マージソートの時間計算量は、平均、最悪ともに\( O ( N \log N) \)と、クイックソートは平均 \( O ( N \log N) \) 、最悪 \( O ( N ^2) \)なので、最悪時間計算量はクイックソートより良いです。

Analysis

クイックソートと異なり安定ソートですが、内部ソートではありません。

ソートのために\( \Theta (N) \) の追加メモリが必要になります。

連結リストのソートに対しては、クイックソートより適しています。

Java では、順序関係は同じでも内実が異なる可能性のあるオブジェクトのソートには安定ソートであるマージソートを、ソートの安定性が意味のないプリミティブにはクイックソートと使い分けているそうです。

Java: Arrays.sort quicksort and mergesort [duplicate]

Python で実装

マージソートを Python で実装します。

import random

def merge_sort(array):
    if len(array) > 1:

        # リストを分割
        middle_index = len(array) // 2
        left_half = array[:middle_index]
        right_half = array[middle_index:]

        # 分割したリストを再帰的にソート
        merge_sort(left_half)
        merge_sort(right_half)
    
        # 返ってきたソート済みのリストを、ソートしながら一つのリストにまとめる。
        i = j = k = 0
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                array[k] = left_half[i]
                i += 1
            else:
                array[k] = right_half[j]
                j += 1
            k += 1

        # まだ残っているものがある場合は処理する。
        while i < len(left_half):
            array[k] = left_half[i]
            i += 1
            k += 1

        while j < len(right_half):
            array[k] = right_half[j]
            j += 1
            k += 1


if __name__ == '__main__':

    random.seed(1)
    array = [random.randrange(100) for i in range(10)]
    print('未ソート', array)
    # 未ソート [17, 72, 97, 8, 32, 15, 63, 97, 57, 60]
    merge_sort(array)
    print('ソート済み', array) 
    # ソート済み [8, 15, 17, 32, 57, 60, 63, 72, 97, 97]