平衡二分探索木
平衡二分探索木(へいこうにぶんたんさくぎ、英: self-balancing binary search tree)とは、計算機科学において二分探索木のうち木の高さ(根からの階層の数)を自動的にできるだけ小さく維持しようとするもの(平衡木)である。平衡二分探索木は連想配列や集合その他の抽象データ型を実装する最も効率のよいデータ構造の1つである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
連結リストの計算量\( O (N) \) は、2分探索木を用いることで平衡木であれば\( O ( \log N) \) に減らすことが出来ました。
しかし、例えばソート済みの配列 [1, 2, 3, 4, 5] で2分探索木を生成した場合、 \( O (N) \) の計算量になってしまいます。
そこで、2分探索木にデータの追加や削除を行った際に、自動的に木を平衡にする仕組みを取り入れることで、常に \( O ( \log N) \) になるデータ構造になります。
こういった木構造は、平衡二分探索木と呼ばれます。
AVL木
AVL木は以前も一度まとめていて、より分かりやすい説明を目指します。
AVL木(えーぶいえるき、AVL tree、Adelson-Velskii and Landis’ tree)とは、コンピュータサイエンスにおいて、「どのノードの左右部分木の高さの差も1以下」という条件を満たす2分探索木のことである。
平衡2分探索木の1つで、木に対する操作によって条件を満たさないノードが発生しても、回転と呼ばれる操作を行うだけで木をAVL木に再構成でき、平衡を維持できる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
AVL木はほとんど2分探索木と同じです。
異なる点は、2分探索木の計算量は「木の高さ」によって決まるので、AVL木では「左右の部分木の高さの差を1以下」にすることで平衡木を作ろうと考える点です。
AVL木は2分探索木と同様に、全てのノードは「左の子の値 ≤ 親 ≤ 右の子の値」 という構造を維持します。また、データの挿入や削除も2分探索木と同様の流れで行われますが、「木が平衡しているかの確認」と「平衡していない場合に平衡させる操作」が2分探索木の操作に加わります。最大値の取得や最小値の取得は2分探索木と同じです。
2分探索木とAVL木の計算量は以下のようになります。
2分探索木の計算量
| 平均 average case | 最悪 worst case | |
|---|---|---|
| 空間計算量 | \( O (N) \) | \( O (N) \) |
| 挿入 | \(O ( \log N )\) | \( O (N) \) |
| 探索 | \(O ( \log N )\) | \( O (N) \) |
| 削除 | \(O ( \log N )\) | \( O (N) \) |
AVL木の計算量
| 平均 average case | 最悪 worst case | |
|---|---|---|
| 空間計算量 | \( O (N) \) | \( O (N) \) |
| 挿入 | \(O ( \log N )\) | \(O ( \log N )\) |
| 探索 | \(O ( \log N )\) | \(O ( \log N )\) |
| 削除 | \(O ( \log N )\) | \(O ( \log N )\) |
AVL木は、2分探索木よりも実行前に計算量が予測できるようになっています。
ノードの高さ
「ノードの高さ」とは、「そのノードをルートと考えた時の部分木の高さ」で、そのノードから一番遠い葉への長さであり、「左右の子の高さの大きい方に1を足したもの」です。
例えば、下のような木であれば、葉である「9」「14」「19」「67」「76」の高さは0、「12」「23」「54」の高さは1、「17」「72」の高さは2、「50」の高さは3になります。
また、AVL木では、葉ノードの子ノード、つまりNullの高さを「-1」と便宜上設定します。
AVL木は、 全ての左右のノードの高さの差の絶対値が常に1以下になるように、「回転」という操作を行います。
例えば、要素の挿入が行われると、まずは2分探索木の挿入によりその要素が挿入されます。
すると、挿入箇所からルートの間にある全てのノードでは、高さが変わった可能性が生じるので、これら全てのノードに対して、 「左右のノードの高さの差の絶対値が1以下 」かどうかを確認を行います。途中「1より大きい」ノードが見つかった場合、「回転」操作で 「左右のノードの高さの差の絶対値が1以下 」 になるように調整します。最終的にルートに辿り着くと、確認調整は終了します。
この操作は木の高さだけ行われるので、\( O ( \log N )\) で行うことができます。
回転
「回転」について具体的に考えます。
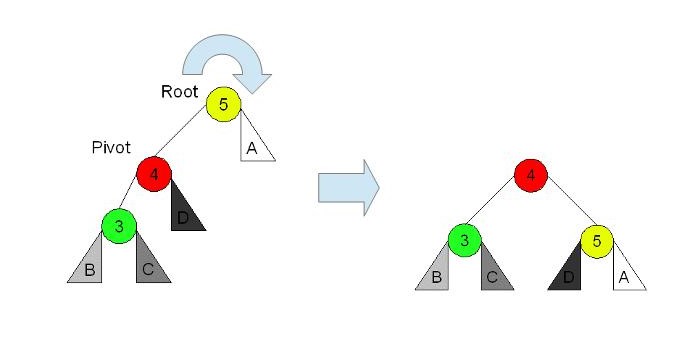
回転とは図示すると以下のような操作で、「右回転」と「左回転」の操作があります。
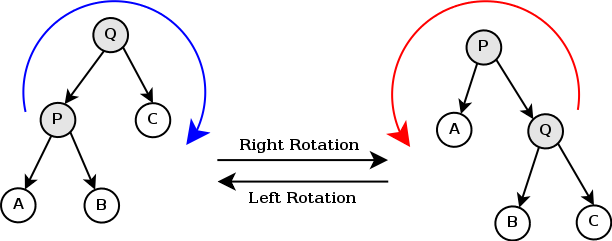
例えば左の木に「右回転」の操作を行うと、ルート「Q」の左側の子の「P」が新しい木のルートになり、「Q」は「P」の右側の子になります。この時、もともと「P」の右側の子であった「B」は「Q」の左側の子となります。
in-order で木を巡回すると、どちらの木とも A – P – B – Q – C という順番を維持しています。
計算量は\( O (1) \) です。
左-左と子がある場合 Left Left Case
下の図のような状況を考えます。
「A」「B」「C」「D」は同じ高さを持つ部分木とします。
ここでは、「A」「B」「C」「D」を Null として考えてみます。
「2」は左右の子は Null 、左右の子の高さの差は「0」です。
「3」は左の子は高さ「0」右の子は Null で高さ「-1」、 左右の子の高さの差は「1」です。
「5」は左の子は高さ「1」右の子は Null で高さ「-1」、 左右の子の高さの差は「2」で不均衡な木になっています。
右回転を行うことで木が均衡します。
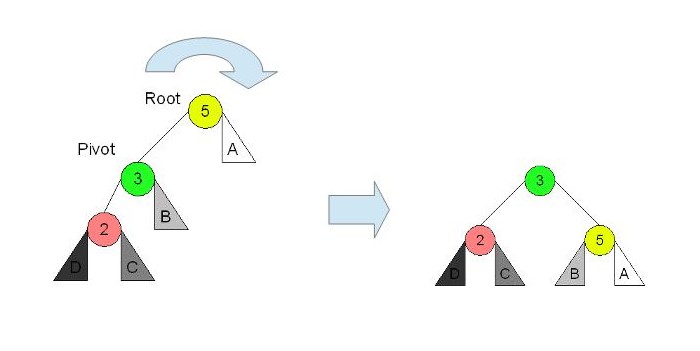
右回転を行うと左右はバランスします。
右-右と子がある場合 Right Right Case
左側に子が2つある場合の逆で、木の均衡を保つため、左回転します。

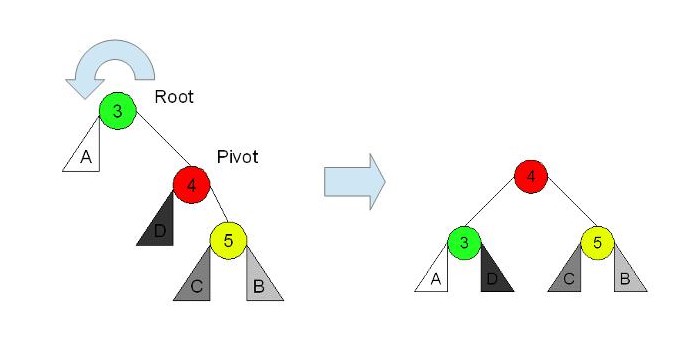
左-右と子がある場合 Left Right Case
下側の部分木で左回転すると、左-左と子がある場合 Left Left Case と同じ状況になるので、あとは同じように右回転することで木の均衡を保つことができます。
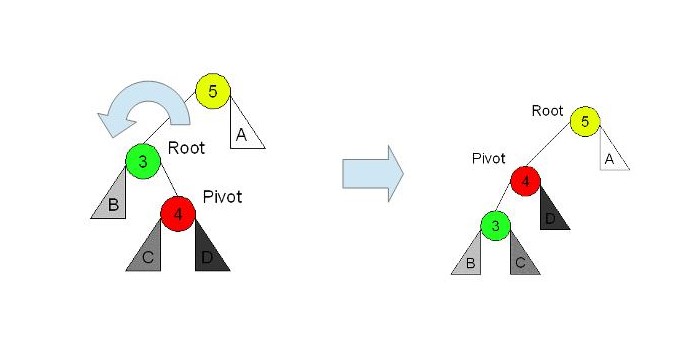
右-左と子がある場合 Right Left Case
下側の部分木で左回転すると、右-右と子がある場合 Right Right Case と同じ状況になるので、あとは同じように左回転することで、 木の均衡を保つことができます。