Python で単回帰分析を行ってみます。
numpy でよりプリミティブに行う方法と、sklearn でより簡単に導出する方法を試します。
scipy にも簡単に線形回帰を行うメソッドが用意されています。
単回帰自体については、以下が分かりやすいです。
線形単回帰
散布図上にばらついている データを,\( y = a + bx \)という直線のモデルで表す場合, 結果として、\( \bar{x} \) \( \bar{y} \) をそれぞれ \( x\)と\(y\) の平均、\( \sigma_{xy} \) を\( x\)と\(y\)の共分散、\( {\sigma_{x}}^2 \)を\(x\)の分散として、
$$ b = \frac { \sigma_{xy} } { {\sigma_{x}}^2 }$$
$$ a = \bar{y} – b \bar{x} $$
と表すことができます。
また、回帰直線のデータへの当てはまり具合を示す決定係数\( r^2 \) は、
$$ r^2 = { ( \frac{ \sigma_{xy} } { \sigma_{x} \sigma_{y}} ) }^2 $$
と、相関係数\( r\) の二乗として表すことができます。
データの準備
ipython で進めていきます。
線形回帰と言えば出てくる下記の有名なデータを使います。
In [1]: from sklearn.datasets import load_boston In [2]: boston = load_boston()
データフレームへの変換
読み込んだデータを、データフレームに変換します。
In [8]: import pandas as pd In [9]: df_boston = pd.DataFrame(boston.data) In [11]: df_boston.columns = boston.feature_names In [12]: df_boston['Price'] = boston.target
データの確認
データの内容を確認します。
In [18]: df_boston.head()
Out[18]:
CRIM ZN INDUS CHAS ... PTRATIO B LSTAT Price
0 0.00632 18.0 2.31 0.0 ... 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 ... 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 ... 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 ... 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 ... 18.7 396.90 5.33 36.2
[5 rows x 14 columns]
In [19]: df_boston.describe()
Out[19]:
CRIM ZN ... LSTAT Price
count 506.000000 506.000000 ... 506.000000 506.000000
mean 3.593761 11.363636 ... 12.653063 22.532806
std 8.596783 23.322453 ... 7.141062 9.197104
min 0.006320 0.000000 ... 1.730000 5.000000
25% 0.082045 0.000000 ... 6.950000 17.025000
50% 0.256510 0.000000 ... 11.360000 21.200000
75% 3.647423 12.500000 ... 16.955000 25.000000
max 88.976200 100.000000 ... 37.970000 50.000000
[8 rows x 14 columns]
In [27]: df_boston.columns
Out[27]:
Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
'PTRATIO', 'B', 'LSTAT', 'Price'],
dtype='object')
価格 Price を目的変数に、部屋の数 RM average number of rooms per dwelling を説明変数とします。
In [34]: df_boston = df_boston[['RM', 'Price']]
In [35]: df_boston.head()
Out[35]:
RM Price
0 6.575 24.0
1 6.421 21.6
2 7.185 34.7
3 6.998 33.4
4 7.147 36.2
In [36]: df_boston.describe()
Out[36]:
RM Price
count 506.000000 506.000000
mean 6.284634 22.532806
std 0.702617 9.197104
min 3.561000 5.000000
25% 5.885500 17.025000
50% 6.208500 21.200000
75% 6.623500 25.000000
max 8.780000 50.000000
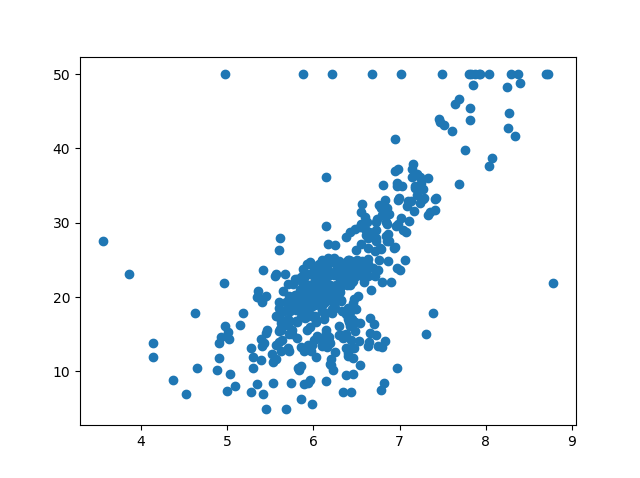
相関係数を確認します。
In [41]: import numpy as np
In [41]: np.corrcoef(df_boston['RM'], df_boston['Price'])
Out[41]:
array([[1. , 0.69535995],
[0.69535995, 1. ]])
大体0.7ぐらいで相関はあります。
散布図を確認します。
In [43]: import matplotlib.pyplot as plt In [44]: plt.scatter(df_boston['RM'], df_boston['Price']); In [45]: plt.show()
回帰直線の導出
$$ b = \frac { \sigma_{xy} } { {\sigma_{x}}^2 }$$
に基づいて、\( b \) を求めます。
まずは、共分散\( \sigma_{xy} \)を求めます。
# df_boston['RM']の平均 In [30]: mean_rm = np.mean(df_boston['RM']) # df_boston['Price']の平均 In [31]: mean_price = np.mean(df_boston['Price']) # 共分散 In [32]: cov_rm_price = np.sum((df_boston['RM'] - mean_rm)*(df_boston['Price'] - mean_price)) * (1/len(df_boston['RM'])) In [33]: cov_rm_price Out[33]: 4.484565551719289
実は、numpy は共分散を求める関数 cov があるので、そちらを使ってみます。
# numpy.cov()による共分散
In [34]: cov_rm_price = np.cov(df_boston['RM'], df_boston['Price'])
In [35]: cov_rm_price
Out[35]:
array([[ 0.49367085, 4.49344588],
[ 4.49344588, 84.58672359]])
なぜか最初と異なる値が出ました…。
ドキュメントを読むと、色々とオプションが設定されるようなので、標本共分散を求めるよう設定します。
In [36]: cov_rm_price = np.cov(df_boston['RM'], df_boston['Price'], ddof=0)
In [37]: cov_rm_price
Out[37]:
array([[ 0.49269522, 4.48456555],
[ 4.48456555, 84.41955616]])
同じ値になりました。
\( {\sigma_{x}}^2 \) を求めます。といっても、上の標本共分散で出てしまっていますが…一応。
# df_boston['RM'] の分散
In [40]: var_rm = np.sum((df_boston['RM'] - mean_rm)**2) * (1/len(df_boston['RM']))
...: var_rm
Out[40]: 0.49269521612976297
# numpy の var() で求めることもできる。
In [41]: np.var(df_boston['RM'])
Out[41]: 0.49269521612976297
b と a を求めます。
In [45]: b = cov_rm_price / var_rm In [46]: b Out[46]: 9.102108981180308 In [47]: a = mean_price - b * mean_rm In [48]: a Out[48]: -34.670620776438554
\( y = -34.670620776438554 + 9.102108981180308 * x \) の直線が導出されました。
図示してみます。
In [57]: x = np.arange(4, 9, 0.01)
In [58]: plt.scatter(df_boston['RM'], df_boston['Price'])
...: plt.plot(x, a + b * x, color='red');
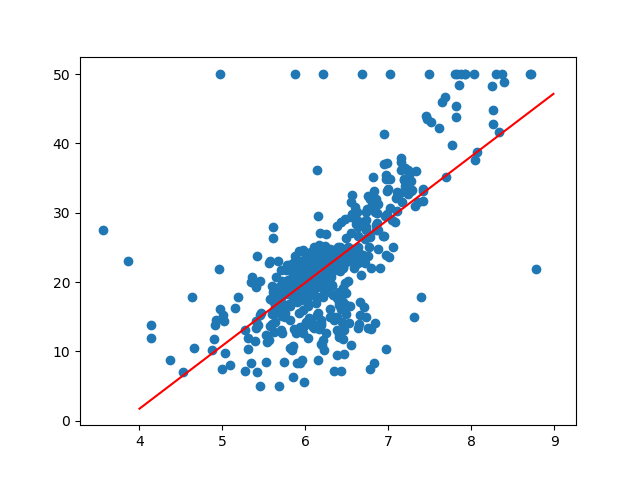
なとなくそれっぽい直線です。
決定係数を計算します。
# 相関係数 In [60]: r = cov_rm_price / (np.std(df_boston['RM']) * np.std(df_boston['Price'])) # 決定係数 In [61]: r**2 Out[61]: 0.4835254559913339
numpy.linalg.lstsq
numpy は最小二乗法を解く関数を持っているので、こちらを使って単回帰の直線を導出してみます。
ちょっと面倒ですが、ドキュメントによると、導く直線を y = Ap と考えて、 A = [[x, 1]] 、 p = [[m], [c]]としなければなりません。
ドキュメントの真似をして書いてみます。
In [72]: A = np.vstack([df_boston['RM'], np.ones(len(df_boston['RM']))]).T In [73]: b, a = np.linalg.lstsq(A, df_boston['Price'])[0] In [74]: b Out[74]: 9.102108981180315 In [75]: a Out[75]: -34.670620776438575
上とほぼ同じ値が導出されました。
sklearn.linear_model.LinearRegression
scikit-learn にも、線形回帰による予測を行うクラスとして、sklearn.linear_model.LinearRegression が用意されているので、こちらを使ってみます。
sklearn.linear_model.LinearRegression
これもドキュメント通りに進めてみます。
In [95]: from sklearn.linear_model import LinearRegression In [96]: x = df_boston[['RM']].values In [97]: y = df_boston['Price'].values In [98]: reg = LinearRegression().fit(x, y) In [99]: reg.coef_[0] Out[99]: 9.10210898118031 In [100]: reg.intercept_ Out[100]: -34.67062077643857
上とほぼ同じ値が導出されました。