2分ヒープ
2分ヒープを理解して、Pythonで実装します。
まず、heap とは、「積み重なった山のようなもの」です。a heap of stones と言えば、石が山のように積み重なっているものです。
ヒープソートは、この山のように積み重なったものの一番上のところから、一つずつものを取っていくイメージです。
二分ヒープ(にぶんヒープ,バイナリヒープ,Binary heap)とは、二分木を使って作られるヒープ(データ構造)の特に単純な種類のひとつである。それは、二分木に、以下の2つの制約を追加したものとみなせる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
以下の動画を参照します。
木構造と配列
まずは、配列を以下のルールに従い木構造で表現することを考えます。
インデックス i のノードがあるとして、
- そのノードの左側の子のインデックスは 2 * i
- そのノードの右側の子のインデックスは 2 * i + 1
- そのノードの親のインデックスは i / 2 (切り下げる)
例えば、以下のような配列を考えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | A | B | C | D | E | F | G |
この配列は、以下の木構造で表現されます。

ノードBを例にすると、左の子Dのインデックスは 2*2=4、右の子Eのインデックスは2*2+1=5、親のAのインデックスは 2/2=1 と上のルールを満たします。
以下のような配列を考えます。
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | A | B | C | D | E |
この配列は、以下の木構造で表現されます。
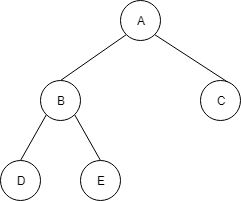
この木構造も、ちゃんと上のルールを満たしています。
以下のような配列を考えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | A | B | C | – | – | F | G |
この配列は、以下の木構造で表現されます。
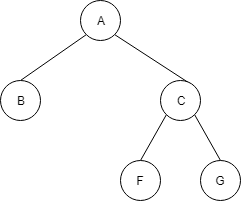
ノードCを例にすると、左の子Fのインデックスは 3*2=6、右の子Gのインデックスは3*2+1=7、親のAのインデックスは 3/2=1(切り下げ) と上のルールを満たします。
完全2分木
動画の説明と異なりますが、完全2分木 ‘complete binary tree’ とは、一番下のレベル以外は、ノードが全て埋まっており、また一番下のレベルのノードがある場合は、可能な限り左側に寄っている2分木です。
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes at the last level h.[18]
complete binary tree
以下は、完全2分木です。
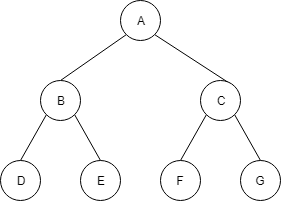
以下も、完全2分木です。
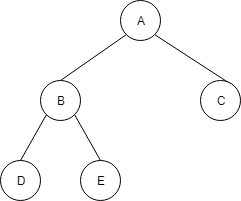
以下は、左側が空いてしまっており、完全2分木ではありません。
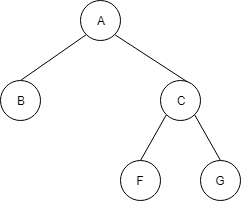
また、全てのノードが埋まっている場合、高さは log n で表すことができます。
ヒープ
ヒープとは、完全2分木であり、 それぞれのノードがそのノードの子よりも大きい(または小さい)という順序関係を満たすようになっているものです。
それぞれのノードがそのノードの子よりも大きい場合は max heap 、小さい場合は min heap と呼びます。
max heap
max heap の例です。
max heap は、それぞれのノードがそのノードの子よりも大きくなります。
また、ルートが一番大きくなります。
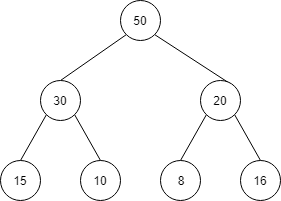
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 50 | 30 | 20 | 15 | 10 | 8 | 16 |
min heap
min heap の例です。
min heap は、それぞれのノードがそのノードの子よりも小さくなります。
また、ルートが一番小さくなります。
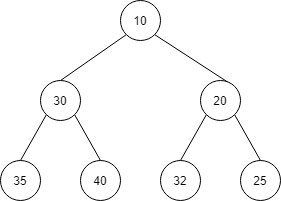
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 10 | 30 | 20 | 35 | 40 | 32 | 25 |
以下では、max heap を考えます。
ノードの挿入
挿入は、まず完全2分木のルールを守るようにノードの挿入場所を確保し、それから順序関係を満たすようにノードの入れ替えを行うという順番で行われます。
以下の木に max heap の条件を満たすように、60を挿入することを考えます。
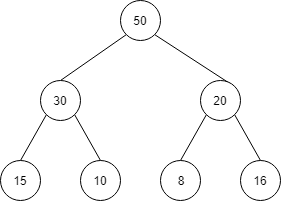
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 値 | 50 | 30 | 20 | 15 | 10 | 8 | 16 |
この場合、まずは、配列の一番右側 index 8 に60を挿入します。
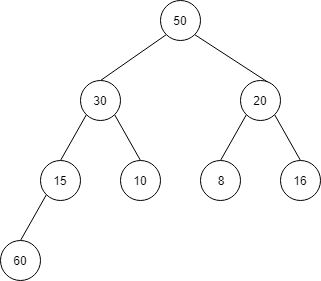
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 値 | 50 | 30 | 20 | 15 | 10 | 8 | 16 | 60 |
その後、下の方から親と値を比較して、親の方が小さい場合は、入れ替えを行います。
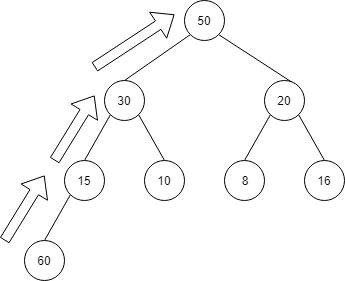
入れ替えが終わると、以下のようになります。
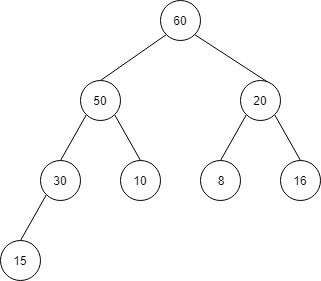
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 値 | 60 | 50 | 20 | 30 | 10 | 8 | 16 | 15 |
この入れ替えは、「木の高さ」だけ行われます。木の高さは log n なので O (log n) で挿入を行うことができます。
また、挿入は、「下から上」という方向で行われます。
ノードの削除
heap からは、ルートだけが削除できます。
heap つまり、山のような積み重なったもの から、一番上のものを取り除くイメージです。
ルートを削除してから、まずは、完全2分木のルールを守るように、一番最後のノードをルートに持ってきて、それから順序関係を満たすようにノードの入れ替えを行うという順番で行われます。
以下から50を削除します。
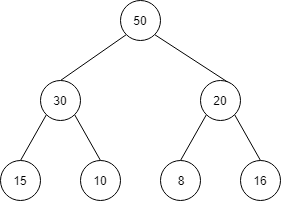
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 50 | 30 | 20 | 15 | 10 | 8 | 16 |
50の場所が空きます。
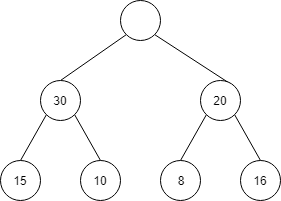
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 30 | 20 | 15 | 10 | 8 | 16 |
50の場所に、一番最後の16を持ってきます。
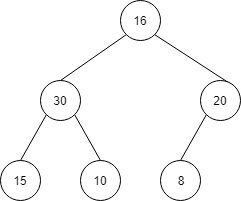
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 16 | 30 | 20 | 15 | 10 | 8 |
順序関係を満たすように、ノードの入れ替えを行います。
まず子の比較を行います。
30と20では、30の方が大きいので、入れ替えが必要な場合は30を親と入れ替えます。
次に、親と子を比較します。
30と16では、30のほうが大きいので、入れ替えを行います。
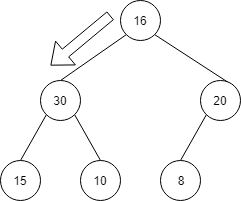
この比較・入れ替えを、上から下にどんどんと進めるイメージです。
続いて、子供の15と10を比較すると15の方が大きいです。
15と16を比較すると、16の方が大きいので、入れ替えの必要はありません。
今回の場合は、一度入れ替えるだけで順序関係が満たされました。
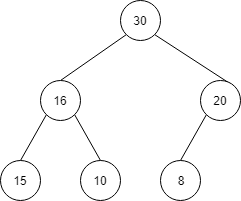
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 30 | 16 | 20 | 15 | 10 | 8 |
今回も、入れ替えは、最悪「木の高さ」だけ行われます。木の高さは log n なので、O (log n) で削除を行うことができます。
ここで、削除した値を、空いた場所に入れると考えます。
例えば、今回の場合は、最初に60が削除され以下のようになります。

| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 30 | 16 | 20 | 15 | 10 | 8 | 60 |
次は30が削除され以下のようになります。
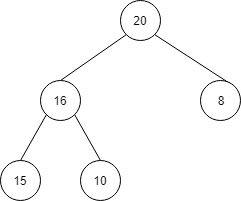
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 20 | 16 | 8 | 15 | 10 | 30 | 60 |
次は20が削除され以下のようになります。
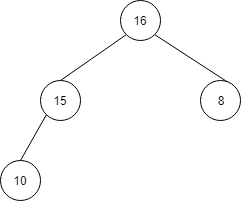
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 16 | 15 | 8 | 10 | 20 | 30 | 60 |
この調子で全て削除していくと、最終的には、以下のようなソートされた配列を得ることができます。
これがヒープソートと呼ばれるソート方法です。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 8 | 10 | 15 | 16 | 20 | 30 | 60 |
ヒープソート
ヒープソートは以下の順番で行われます。
- ヒープを作る。
- ヒープから全ての値を削除する。
下の配列を使ってヒープソートを行ってみます。
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 10 | 20 | 15 | 30 | 40 |
まずは10を挿入します。

| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 10 |
次に20を挿入します。
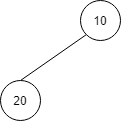
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 10 | 20 |
順序関係が保たれるように、10と20を交換します。
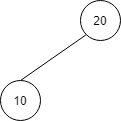
…
この流れで、値を挿入していくと、最終的に以下のようになります。
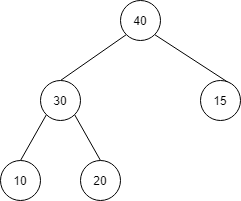
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 40 | 30 | 15 | 10 | 20 |
ここまでで、n 個のノードを挿入するのに、それぞれのノードで log n 回の操作が必要になり、ヒープの作成で n * log n の時間がかかります。
ここから、ノードの削除を行います。
まずは40を削除し、20をルートに持ってきて、さらに順序関係を満たすように入れ替えを行います。
削除した40は配列の空いたスペースに持ってきます。
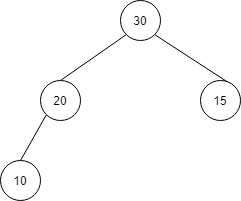
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 30 | 20 | 15 | 10 | 40 |
続いて30を削除し、10をルートに持ってきて、順序関係を満たすように入れ替えを行います。

| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 20 | 10 | 15 | 30 | 40 |
…
この流れで削除していくと、最終的に以下のような、ソートされた配列を得ることができます。
| index | 1 | 2 | 3 | 4 | 5 |
| 値 | 10 | 15 | 20 | 30 | 40 |
削除についても挿入と同じく、n 個のノードを削除するのに、それぞれのノードで log n 回の操作が必要になり、ヒープの作成で n * log n の時間がかかります。
つまり、ヒープソートは O (n log n) になります。
heapify
heapify は、配列からのヒープの生成を部分木ことに見て行う方法です。
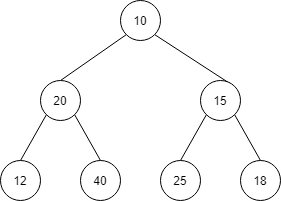
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 10 | 20 | 15 | 12 | 40 | 25 | 18 |
一番最後のノードから、そのノードをルートと考えて、ヒープ構造を満たしているかを確認していきます。
最初は18で、これは単独のノードなので、ヒープ構造を満たしています。
25、40、12も、18と同じく、単独のノードで、ヒープ構造を満たしています。
次に15に進みます。
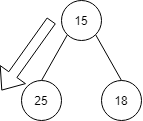
15はヒープ構造を満たないので、15と25の入れ替えが発生します。
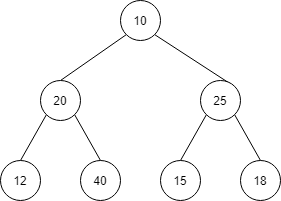
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 10 | 20 | 25 | 12 | 40 | 15 | 18 |
20に進みます。
これもヒープ構造を満たさず、20と40の入れ替えが発生します。
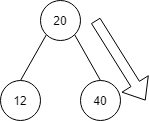
下のようになります。
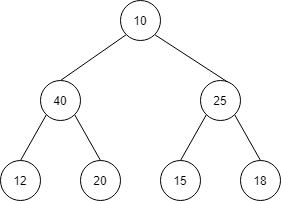
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 10 | 40 | 25 | 12 | 20 | 15 | 18 |
10に進みます。
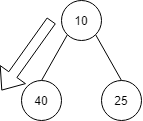
これもヒープ構造を満たさず、10と40の入れ替えを行います。
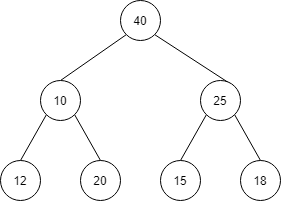
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 40 | 10 | 25 | 12 | 20 | 15 | 18 |
続いて、10と20の入れ替えを行います。
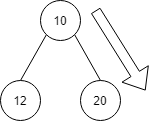
以下のように、ヒープを満たす構造が完成します。
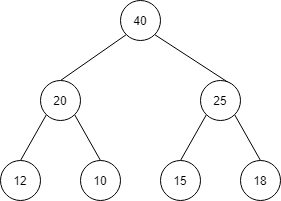
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 40 | 20 | 25 | 12 | 10 | 15 | 18 |
以前の方法では、ノードの挿入を行うたびに木の調整を行いましたが、この方法では、木を生成してから、部分木ごとにヒープ構造が守られているかの確認・調整を行います。
優先度付きキュー
また、ヒープを使うことで、優先度付きキューを作ることができます。
優先度付きキュー(ゆうせんどつき -、英: priority queue)は、以下の4つの操作をサポートする抽象データ型である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
– キューに対して要素を優先度付きで追加する。
– 最も高い優先度を持つ要素をキューから取り除き、それを返す。
– (オプション) 最も高い優先度を持つ要素を取り除くことなく参照する。
– (オプション) 指定した要素を取り除くことなく優先度を変更する
通常のキューは、FIFOで処理されますが、優先度付きキューは、優先度の高いものから順に処理をしていくキューです。
「最も高い優先度を持つ要素をキューから取り除き、それを返す」という処理は、ヒープの削除操作そのものです。
2分ヒープを使うことで、要素の挿入・削除をO(log n)、先頭の参照や取得はO(1)で行うことができる優先度付きキューになります。
以下に続きます。
