[Pyhon] AVL木

以下を参照しています。

AVL Tree | Set 1 (Insertion)

AVL Tree | Set 2 (Deletion)

また、ざっくりとした説明は、以下の動画が一番分かりやすかったです。

インドの人は説明が上手です。

10.1 AVL Tree – Insertion and Rotations

AVL木

AVL木（えーぶいえるき、AVL tree、Adelson-Velskii and Landis’ tree）とは、コンピュータサイエンスにおいて、「どのノードの左右部分木の高さの差も1以下」という条件を満たす2分探索木のことである。

出典: フリー百科事典『ウィキペディア（Wikipedia）』

探索の計算量が、常に \( O (\log n)\)程度になるように改良された2分探索木です。

左右の部分木の高さの差を「平衡係数」として、その差の絶対値が常に1以下になるように、回転という操作を行います。

平衡係数と回転の操作以外は、2分探索木と同じです。

回転

AVL木にノードの挿入や削除といった変化があり、平衡が保たれなくなった場合、回転という操作を行って、平衡を保ちます。

回転

回転とは以下のような操作です。

inorderで巡回すると、 回転の操作を行っても、双方とも A – P – B – Q – C という順番になっていることがわかります。

なので、どちらかが2分探索木であれば、回転を行った後の木も、2分探索木となります。

ノードの挿入

wというノードの挿入を考えます。

1) wを、まずは通常の2分探索木の挿入方法で挿入します。
2) 挿入したノードwからルートに向かって進みます。最初の平衡していないノードが見つかったら、それをzとします。zからwへの通路上にある最初のzの子要素をy、yの子要素をxとします。
3) 部分木のルートをzとして、平衡を取り戻すための回転の操作を行います。yとxの位置関係によって、以下の4つの操作に分かれます。
　a) yがzの左側の子要素で、xはyの左側の子要素である。(Left Left Case)
　b) yがzの左側の子要素で、xはyの右側の子要素である。(Left Right Case)
　c) yがzの右側の子要素で、xはyの右側の子要素である。(Right Right Case)
　d) yがzの右側の子要素で、xはyの左側の子要素である。 (Right Left Case)

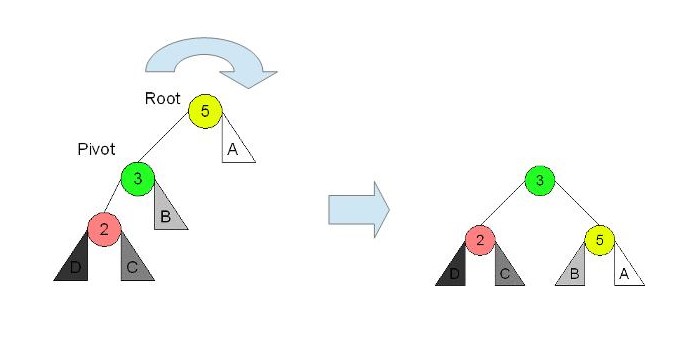
a) yがzの左側の子要素で、xはyの左側の子要素である。(Left Left Case)

zが5、yが3、xは2と考えます。

Pivotはその回転で新しくrootになるノードです。

右回転します。

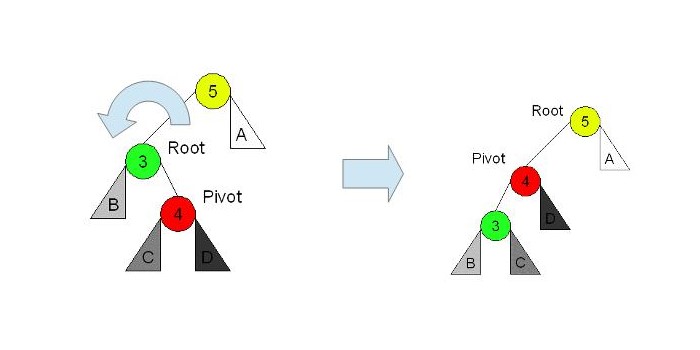
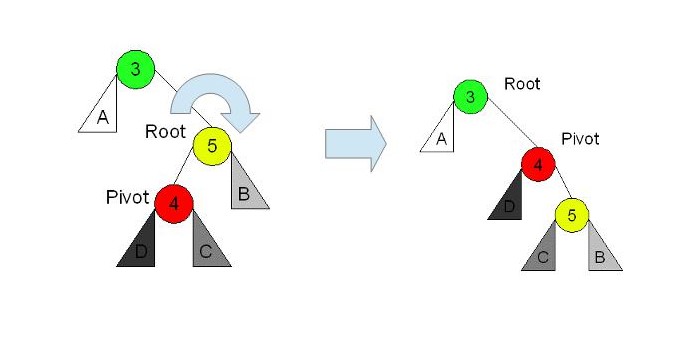
b) yがzの左側の子要素で、xはyの右側の子要素である。(Left Right Case)

zが5、yが3、xは4と考えます。

Pivotはその回転で新しくrootになるノードです。

左回転します。

右回転します。

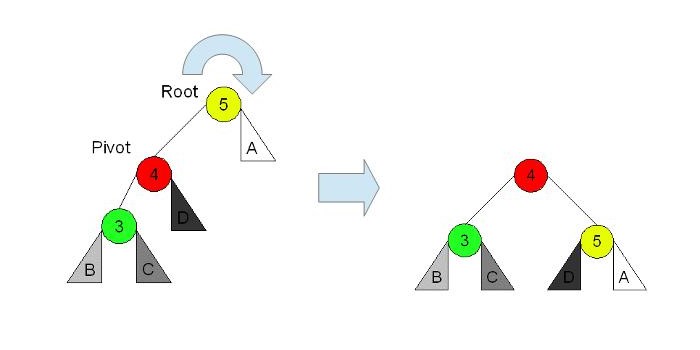
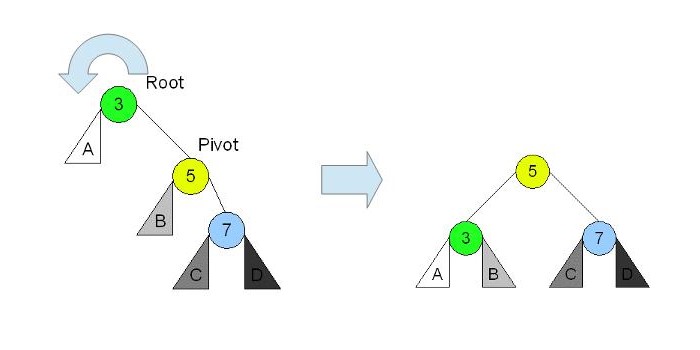
c) yがzの右側の子要素で、xはyの右側の子要素である。(Right Right Case)

zが3、yが5、xは7と考えます。

Pivotはその回転で新しくrootになるノードです。

左回転します。

d) yがzの右側の子要素で、xはyの左側の子要素である。 (Right Left Case)

zが3、yが5、xは4と考えます。

Pivotはその回転で新しくrootになるノードです。

右回転します。

左回転します。

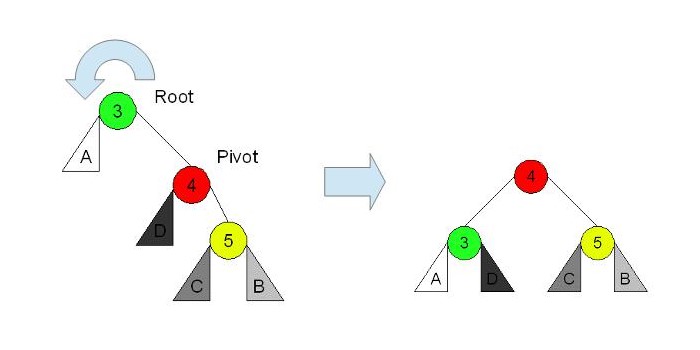
ノードの挿入のアルゴリズム

2分探索木の挿入は再帰的に行うとします。

1) 2分探索木の挿入を再帰的に行う。
2) 現在のノードは新しく挿入されたノードの祖先になっている。現在のノードの高さを更新する。
3) 現在のノードの平衡係数（左の部分木の高さ – 右の部分木の高さ）を取得する。
4) 平衡係数が1より大きい場合は、現在のノードは不均衡なので、 Left Left case か left Right case の回転を行う。どちらの回転に該当するのか、新しく挿入した値と 現在のノードの左の子の値を比較し、新しく挿入した値 < 左の子の値 であれば、 Left Left case の回転、 新しく挿入した値 > 左の子の値 であれば Left Right case の回転を行う。
5) 平衡係数-1より小さい場合は、 現在のノードは不均衡なので、 Right Right case か Right Left case の回転を行う。どちらの回転に該当するのか、新しく挿入した値と現在のノードの右の子の値を比較し、新しく挿入した値 > 右の子の値 であれば、 Right Right case の回転、 新しく挿入した値 < 右の子の値 であれば Right-Left case の回転を行う。

ノードの削除

1) 通常の2分探索木の挿入方法で削除します。
2) 挿入したノードwからルートに向かって進みます。最初の平衡していないノードが見つかったら、それをzとします。挿入とは異なり、zの子ノードで高さが高いほうの子をy、yの子ノードで高さが高いほうをxとします。
3) 部分木のルートをzとして、平衡を取り戻すための回転の操作を行います。yとxの位置関係によって、以下の4つの操作に分かれます。
　a) yがzの左側の子要素で、xはyの左側の子要素である。(Left Left Case)
　b) yがzの左側の子要素で、xはyの右側の子要素である。(Left Right Case)
　c) yがzの右側の子要素で、xはyの右側の子要素である。(Right Right Case)
　d) yがzの右側の子要素で、xはyの左側の子要素である。 (Right Left Case)

ノードの削除のアルゴリズム

1) 2分探索木の削除を行う。
2) 現在のノードは削除されたノードの祖先になっている。現在のノードの高さを更新する。
3)  現在のノードの平衡係数（左の部分木の高さ – 右の部分木の高さ）を取得する。
4)  平衡係数が1より大きい場合は、現在のノードは不均衡なので、 Left Left case か left Right case の回転を行う。左の子の平衡係数を取得し、左の子の平衡係数が0より大きいかまたは0の場合は Left Left case 、そうでない場合は Left Right case の回転を行う。
5)  平衡係数が1より小さい場合は、現在のノードは不均衡なので、 Left Left case か left Right case の回転を行う。左の子の平衡係数を取得し、左の子の平衡係数が0より大きいかまたは0の場合は Right Right case 、そうでない場合は Right Left case の回転を行う。

Pythonでの実装

class TreeNode(object): 
	def __init__(self, val): 
		self.val = val 
		self.left = None
		self.right = None
		self.height = 1


class AVL_Tree(object): 

	def insert(self, root, key): 
	
		# 2分探索木の挿入を再帰的に行う。
		if not root: 
			return TreeNode(key) 
		elif key < root.val: 
			root.left = self.insert(root.left, key) 
		else: 
			root.right = self.insert(root.right, key) 

		# Step 2 - 現在のノードは新しく挿入されたノードの祖先になっている。現在のノードの高さを更新する。
		root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) 

		# Step 3 - 現在のノードの平衡係数（左の部分木の高さ – 右の部分木の高さ）を取得する。
		balance = self.getBalance(root) 

		# Step 4 - 
        # 平衡係数が1より大きい場合は、現在のノードは不均衡なので、 Left Left case か left Right case の回転を行う。
        # 平衡係数-1より小さい場合は、 現在のノードは不均衡なので、 Right Right case か Right Left case の回転を行う。
		# Case 1 - Left Left 
		if balance > 1 and key < root.left.val: 
			return self.rightRotate(root) 

		# Case 2 - Right Right 
		if balance < -1 and key > root.right.val: 
			return self.leftRotate(root) 

		# Case 3 - Left Right 
		if balance > 1 and key > root.left.val: 
			root.left = self.leftRotate(root.left) 
			return self.rightRotate(root) 

		# Case 4 - Right Left 
		if balance < -1 and key < root.right.val: 
			root.right = self.rightRotate(root.right) 
			return self.leftRotate(root) 

		return root 
	
	def delete(self, root, key): 

		# Step 1 - 2分木探索の削除を再帰的に行う。
		if not root: 
			return root 

		elif key < root.val: 
			root.left = self.delete(root.left, key) 

		elif key > root.val: 
			root.right = self.delete(root.right, key) 

		else: 
			if root.left is None: 
				temp = root.right 
				root = None
				return temp 

			elif root.right is None: 
				temp = root.left 
				root = None
				return temp 

			temp = self.getMinValueNode(root.right) 
			root.val = temp.val 
			root.right = self.delete(root.right, temp.val) 

		# 現在のノードが葉の場合は以下の処理は必要ない。
		if root is None: 
			return root 

		# Step 2 - 現在のノードは新しく挿入されたノードの祖先になっている。現在のノードの高さを更新する。
		root.height = 1 + max(self.getHeight(root.left), 
							self.getHeight(root.right)) 

		# Step 3 - 現在のノードの平衡係数（左の部分木の高さ – 右の部分木の高さ）を取得する。
		balance = self.getBalance(root) 

		# Step 4 - If the node is unbalanced, 
		# then try out the 4 cases 
		# Case 1 - Left Left 
		if balance > 1 and self.getBalance(root.left) >= 0: 
			return self.rightRotate(root) 

		# Case 2 - Right Right 
		if balance < -1 and self.getBalance(root.right) <= 0: 
			return self.leftRotate(root) 

		# Case 3 - Left Right 
		if balance > 1 and self.getBalance(root.left) < 0: 
			root.left = self.leftRotate(root.left) 
			return self.rightRotate(root) 

		# Case 4 - Right Left 
		if balance < -1 and self.getBalance(root.right) > 0: 
			root.right = self.rightRotate(root.right) 
			return self.leftRotate(root) 

		return root 
	

	def leftRotate(self, z): 

        #     z                               y     
        #    /  \                            / \   
        #   T1   y                          z   T3    
        #       / \     - - - - - - - >    / \     
        #     T2  T3     Left Rotation    T1  T2   

		y = z.right 
		T2 = y.left 

		# 回転を行う。
		y.left = z 
		z.right = T2 

		# 高さを更新する。
		z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) 
		y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) 

		# 新しいrootを返す。 
		return y 

	def rightRotate(self, z): 
        
        #      z                               y
        #     / \     Right Rotation          /  \
        #    y   T3   - - - - - - - >        T1   z 
        #   / \                                  / \
        #  T1  T2                               T2  T3

		y = z.left 
		T3 = y.right 

		# 回転を行う。
		y.right = z 
		z.left = T3 

		# 高さを更新する。 
		z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) 
		y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) 

		# 新しいrootを返す。
		return y 

	def getHeight(self, root): 
		if not root: 
			return 0

		return root.height 

	def getBalance(self, root): 
		if not root: 
			return 0

		return self.getHeight(root.left) - self.getHeight(root.right) 

	def getMinValueNode(self, root): 
		if root is None or root.left is None: 
			return root 

		return self.getMinValueNode(root.left) 

	def inOrder(self, root): 

		if not root: 
			return

		self.inOrder(root.left) 
		print("{} ".format(root.val), end="") 
		self.inOrder(root.right) 
	
	def preOrder(self, root): 

		if not root: 
			return

		print("{} ".format(root.val), end="") 
		self.preOrder(root.left) 
		self.preOrder(root.right) 

	


myTree = AVL_Tree() 
root = None

root = myTree.insert(root, 10) 
root = myTree.insert(root, 20) 
root = myTree.insert(root, 30) 
root = myTree.insert(root, 40) 
root = myTree.insert(root, 50) 
root = myTree.insert(root, 25) 
root = myTree.insert(root, 5) 
root = myTree.insert(root, 35)

"""The constructed AVL Tree would be 
		　 30 
		　/  \ 
		20  　 40 
		/ \	   / \ 
	　10 　25 35　50
	 /
	5
"""

# Inorder Traversal 
# 5 10 20 25 30 35 40 50
print("Inorder traversal of the constructed AVL tree is") 
myTree.inOrder(root) 
print() 
# Preorder Traversal 
# 30 20 10 5 25 40 35 50
print("Preorder traversal of the constructed AVL tree is") 
myTree.preOrder(root) 
print() 

root = myTree.delete(root, 50) 
root = myTree.delete(root, 40)

"""The constructed AVL Tree would be 
		　 20
		　/  \ 
		10  　 30
		/     / \ 
	　5 　　 25  35
"""

# Inorder Traversal 
# 5 10 20 25 30 35
print("Inorder traversal of the constructed AVL tree is") 
myTree.inOrder(root) 
print() 
# Preorder Traversal 
# 20 10 5 30 25 35
print("Preorder traversal of the constructed AVL tree is") 
myTree.preOrder(root) 
print()