ベルマンフォード法
ベルマン–フォード法 (英: Bellman–Ford algorithm) は、重み付き有向グラフにおける単一始点の最短経路問題を解くラベル修正アルゴリズム[1]の一種である。各辺の重みは負数でもよい。辺の重みが非負数ならば優先度付きキューを併用したダイクストラ法の方が速いので、ベルマン–フォード法は辺の重みに負数が存在する場合に主に使われる。名称は開発者であるリチャード・E・ベルマンと Lester Ford, Jr. にちなむ。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ダイクストラ法と同じ最短経路を探すアルゴリズムです。
ベルマンフォード法の計算量は\( O (V \times E)\)と \( O((E+V)×logV) \)の
ダイクストラ法より低速ですが、「負の重みのある辺」を扱うことができます。
下のような負の重みのあるグラフを考えます。
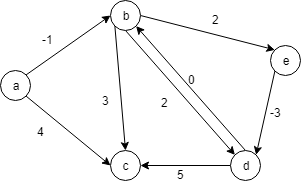
ダイクストラ法は「貪欲法」で最小距離のノードを選び距離の更新を行うことで、最適解に辿り着きました。
しかしこのグラフでダイクストラ法を使うと、(d, b, e)という経路の重みの総和が負になっているため、最短距離の更新が無限に行われます。このような、経路の重みの総和が負になる経路を「負の閉路」と呼び、ダイクストラ法で解くことができません。
ベルマンフォード法は、全てのノードで距離の更新(この距離の更新のことを、ベルマンフォード法では ‘relax’ と言います)を「ノード総数」だけ行うことで、もしグラフ内に「負の閉路」がある場合は、その存在を検知することができます。
『全ての閉路が負でない場合、「ノード総数-1」 回の最短距離の更新後、それ以上最短距離は短くならない』ということが証明できるので、ベルマンフォード法では、 「ノード総数-1」 回の更新後にもう一度更新を行い距離が短くなる場合は、負の経路があると判断します。
また、ダイクストラ法と同じくscipyで実装されているので、Pythonで簡単に使うことができます。
scipy.sparse.csgraph.bellman_ford
疑似コード
ダイクストラ法と良く似ています。
wikipediaの疑似コードに沿って、グラフをノードとエッジを使うことで表現しています。
function BellmanFord(nodes, edges, start):
# グラフの初期化
for n in nodes:
distance[n] = infinity
# 最短経路での前のノード
predecessor[n] = None
distance[start] = 0
# edge の relax を num_nodes - 1 回反復
# 全ての edge に対して、もしその edge で最短経路が短くなるならその距離に更新
for i=1 to num_nodes-1:
for each edge(u, v) with weight w in edges:
temp_distacne = distance[u] + weight
if temp_distance < ditance[v]:
distance[v] = temp_distance
predecessor[v] = u
# 負の閉路の確認
# 閉路がない場合、経路は最長で num_nodes - 1 の edge からなる。
# よって、num_nodes - 1 の edge を確認した後、さらに経路が短くなることは、
# 閉路がある場合を除き考えられない
for each edge(u, v) with weight w in edges:
if distance[u] + w < distance[v]:
Negative Cycle is detected
Python で実装
モジュールのインポート
最短距離を無限大で初期化するため、sys.maxsize を使います。
import sys
ノードとエッジ
疑似コードに従い、ノードとエッジを別のクラスで定義しました。
import sys
class Node(object):
def __init__(self, name):
self.name = name
self.predecessor = None
self.min_distance =sys.maxsize
class Edge(object):
def __init__(self, weight, from_node, to_node):
self.weight = weight
self.from_node = from_node
self.to_node = to_node
距離計算
疑似コードそのままです。
import sys
class Node(object):
def __init__(self, name):
self.name = name
self.predecessor = None
self.min_distance =sys.maxsize
class Edge(object):
def __init__(self, weight, from_node, to_node):
self.weight = weight
self.from_node = from_node
self.to_node = to_node
class BellmanFord(object):
def __init__(self, nodes, edges, start_node):
self.nodes = nodes
self.edges = edges
self.start_node = start_node
self.has_cycle = False
def calculate_shotesht_path(self):
self.start_node.min_distance = 0
for _ in range(len(self.nodes)-1):
for edge in self.edges:
u = edge.from_node
v = edge.to_node
temp_distance = u.min_distance + edge.weight
if temp_distance < v.min_distance:
v.min_distance = temp_distance
v.predecessor = u
for edge in self.edges:
if self.detect_cycle(edge):
self.has_cycle = True
return
def detect_cycle(self, edge):
if (edge.from_node.min_distance + edge.weight) < edge.to_node.min_distance:
return True
return False
def show_shotest_path(self, goal):
if self.has_cycle:
print('This Graph has a negative cycle.')
return False
current_node = goal
order_list = []
while current_node is not None:
order_list.append(current_node.name)
current_node = current_node.predecessor
print(f'from {self.start_node.name} to {goal.name} distance {goal.min_distance}', order_list[::-1])
テスト
以下の3つのグラフの探索を行います。
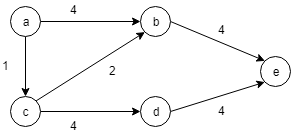
a を出発地点、e を目的地とした場合、最短経路は「a -> c -> b -> e」、移動距離は7 。
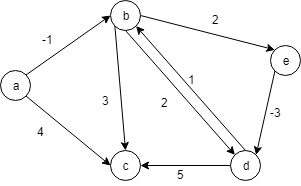
a を出発点、d を目的地とすると、 a から d への最短移動経路: [‘a’, ‘b’, ‘e’, ‘d’] 、移動距離は -2。
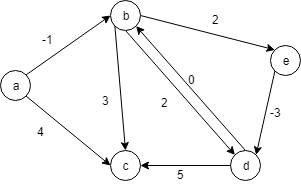
負の閉路が検出される。
import sys
class Node(object):
def __init__(self, name):
self.name = name
self.predecessor = None
self.min_distance =sys.maxsize
class Edge(object):
def __init__(self, weight, from_node, to_node):
self.weight = weight
self.from_node = from_node
self.to_node = to_node
class BellmanFord(object):
def __init__(self, nodes, edges, start_node):
self.nodes = nodes
self.edges = edges
self.start_node = start_node
self.has_cycle = False
def calculate_shotesht_path(self):
self.start_node.min_distance = 0
for _ in range(len(self.nodes)-1):
for edge in self.edges:
u = edge.from_node
v = edge.to_node
temp_distance = u.min_distance + edge.weight
if temp_distance < v.min_distance:
v.min_distance = temp_distance
v.predecessor = u
for edge in self.edges:
if self.detect_cycle(edge):
self.has_cycle = True
return
def detect_cycle(self, edge):
if (edge.from_node.min_distance + edge.weight) < edge.to_node.min_distance:
return True
return False
def show_shotest_path(self, goal):
if self.has_cycle:
print('This Graph has a negative cycle.')
return False
current_node = goal
order_list = []
while current_node is not None:
order_list.append(current_node.name)
current_node = current_node.predecessor
print(f'from {self.start_node.name} to {goal.name} distance {goal.min_distance}', order_list[::-1])
if __name__ == '__main__':
# 負の辺無し
a = Node('a')
b = Node('b')
c = Node('c')
d = Node('d')
e = Node('e')
edge1 = Edge(4, a, b)
edge2 = Edge(1, a, c)
edge3 = Edge(4, b, e)
edge4 = Edge(2, c, b)
edge5 = Edge(4, c, d)
edge6 = Edge(4, d, e)
nodes = [a, b, c, d, e]
edges = [edge1, edge2, edge3, edge4, edge5, edge6]
bellmanford = BellmanFord(nodes, edges, a)
bellmanford.calculate_shotesht_path()
# from a to e distance 7 ['a', 'c', 'b', 'e']
bellmanford.show_shotest_path(e)
# 負の辺あり 閉路無し
a = Node('a')
b = Node('b')
c = Node('c')
d = Node('d')
e = Node('e')
edge1 = Edge(-1, a, b)
edge2 = Edge(4, a, c)
edge3 = Edge(3, b, c)
edge4 = Edge(2, b, d)
edge5 = Edge(2, b, e)
edge6 = Edge(1, d, b)
edge7 = Edge(5, d, c)
edge8 = Edge(-3, e, d)
nodes = [a, b, c, d, e]
edges = [edge1, edge2, edge3, edge4, edge5, edge6, edge7, edge8]
bellmanford = BellmanFord(nodes, edges, a)
bellmanford.calculate_shotesht_path()
# from a to d distance -2 ['a', 'b', 'e', 'd']
bellmanford.show_shotest_path(d)
# 負の辺あり 閉路あり
a = Node('a')
b = Node('b')
c = Node('c')
d = Node('d')
e = Node('e')
edge1 = Edge(-1, a, b)
edge2 = Edge(4, a, c)
edge3 = Edge(3, b, c)
edge4 = Edge(2, b, d)
edge5 = Edge(2, b, e)
edge6 = Edge(0, d, b)
edge7 = Edge(5, d, c)
edge8 = Edge(-3, e, d)
nodes = [a, b, c, d, e]
edges = [edge1, edge2, edge3, edge4, edge5, edge6, edge7, edge8]
bellmanford = BellmanFord(nodes, edges, a)
bellmanford.calculate_shotesht_path()
# This Graph has a negative cycle.
bellmanford.show_shotest_path(d)
想定通りの結果になりました。

