債券(さいけん、英: Bond)とは、社会的に一定の信用力のある発行体が資金を調達する際に、金銭消費貸借契約類似の法律関係に基づく金銭債権の内容を券面上に実体化させて発行する有価証券のこと。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
債券とは、有体に言ってしまえば、「借金の証文」のことです。
例えば、100万円年利10%でお金を貸すことを考えます。
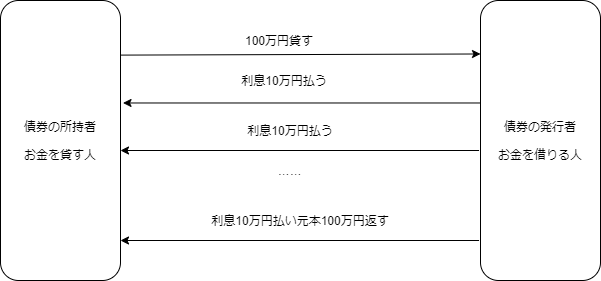
債券の所持者は、債券の発行者に最初に100万円を貸します。
債券の発行者は、債券の満期日までは、債券の所持者に毎年10万円の利息を支払います。
債券の満期日に、債券の発行者は、債券の所持者に、元本の100万円を返し利息10万円を支払うことで、債券は償還されます。
このように、債券は所持することで将来キャッシュフローを得ることができるので、現在の債券の価格は、その債券を所持することで将来生じるキャッシュフローの現在割引価値の総和として考えることができます。
つまり、ある債券の\(t_1, t_2, \cdots , t_n\)で支払われる金額を\(c_1, c_2, \cdots , c_n\)、割引率\(d(t_1), d(t_2), \cdots , d(t_n)\)とすると、 債券価格\(P\)は以下のように表すことができます。
$$ P = \displaystyle \sum_{i=1}^n d(t_i)c_i $$
具体的に、額面100,000円、利率5%、3年に償還される無リスクの債券について、リスクフリーレートが10%の場合の現在割引価値を考えます。
この債券で将来生じるキャッシュフローは、
$$ c_1 = c_2 = 5, 000 $$
$$ c_3 = 105, 000 $$
となります。
それぞれの割引率は、
$$ d(t_1) = \frac{1}{1+0.1} \fallingdotseq 0.90909 $$
$$ d(t_2) = \frac{1}{(1+0.1)^2} \fallingdotseq 0.82645 $$
$$ d(t_3) = \frac{1}{(1+0.1)^3} \fallingdotseq 0.75131 $$
よって、この債券の現在割引価値は、
$$ \begin{align} P &= \displaystyle \sum_{i=1}^3 d(t_i)c_i \\ &= 0.90909 \cdot 5,000 + 0.82645 \cdot 5,000 + 0.75131 \cdot 105,000 \\ & \fallingdotseq 87,565 \end{align} $$