問題
応用情報技術者平成23年特別 午前問24
NAND素子を用いた次の組合せ回路の出力Z を表す式はどれか。ここで、・は論理積、+は論理和、\(\overline{X}\) は \(X\) の否定を表す。
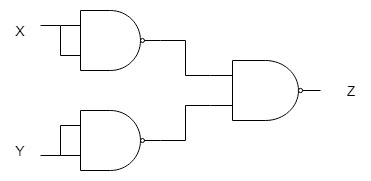
- \(X \cdot Y\)
- \( X + Y\)
- \(\overline{X \cdot Y}\)
- \(\overline{X + Y} \)
答え
\( X + Y\)
解説
NAND
NANDゲートは否定論理積の論理ゲートであり、その(論理的な)動作は全ての入力の論理積(AND)をとったものの反転(NOT)である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
最初のNAND、つまり\(\overline{X \cdot X}\)を考えます。
| \(X\) | \(X\) | \(X \cdot X\) | \(\overline{X \cdot X}\) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 |
ただ反転しているだけです。否定と同じです。
\(\overline{Y \cdot Y}\)も同様に、ただ反転するだけです。
最後のNAND、つまり \( \overline{\overline{X \cdot X} \cdot \overline{Y \cdot Y} } \) を考えます。
| \(X\) | \(Y\) | \(\overline{X \cdot X}\) | \(\overline{Y \cdot Y}\) | \( \overline{X \cdot X} \cdot \overline{Y \cdot Y} \) | \( \overline{\overline{X \cdot X} \cdot \overline{Y \cdot Y} } \) |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
よって、 \( X + Y\) と等しくなります。
または、以下のようにド・モルガンの公式で式変形を行うこともできます。
$$ \begin{align} Z &= \overline{\overline{X \cdot X} \cdot \overline{Y \cdot Y} } \\\\ & = \overline {\overline{X \cdot X}} + \overline {\overline{Y \cdot Y}} \tag{ド・モルガンの公式} \\\\ &= X \cdot X + Y \cdot Y \\\\ &= X + Y \end{align} $$
図版作成ツール
ちなみに、論理回路の図の作成は以下のサイトを使いました。
とても便利です。