問題
応用情報技術者平成22年春期 午前問2
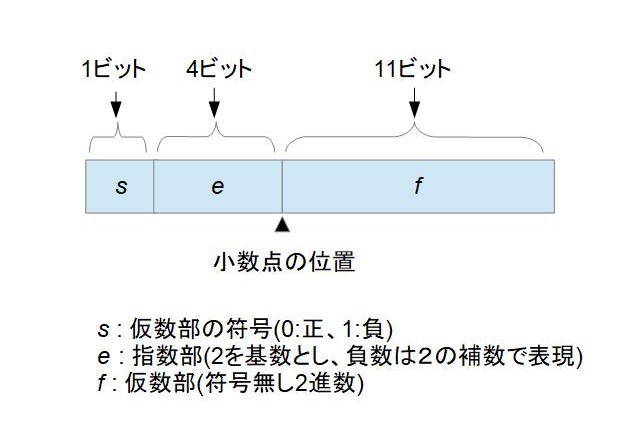
図に示す16ビットの浮動小数点形式において,10進数 0.25 を正規化した表現はどれか。ここで,正規化は仮数部の最上位けたが1になるように指数部と仮数部を調節する操作とする。
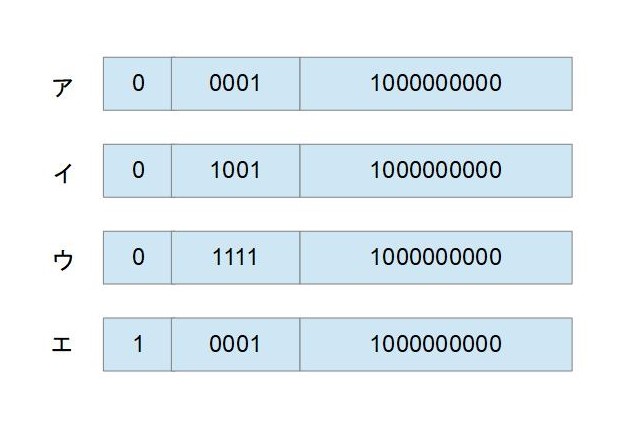
答え

解説
浮動小数点
浮動小数点数(ふどうしょうすうてんすう、英: floating point number)は、浮動小数点方式による数のことで、もっぱらコンピュータの数値表現において、それぞれ固定長の仮数部と指数部を持つ、数値の表現法により表現された数である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
何を言っているのが良く分かりません。
以下が良く分かります。
ただし、問題はIEEE754規格の浮動小数点とは異なります。
2の補数
2の補数(にのほすう)は、2、ないし2のべき乗の補数、またそれによる負の値の表現法である。特に二進法で使われる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
これも何を言っているのか良く分かりません。
以下が良く分かります。
問題を解く
問題を解きます。
まず、0.25は正の数なので、符号はプラス、つまり仮数部の符号sは0になります。
次に、10進数0.25を2進数に変換します。
$$ 0.25(10) = 2 ^ {-2} (10) =0.01(2)$$
次に、2進数0.01を正規化します。
正規化の第一ステップとして、最上位桁が1になるように変形して、仮数部を求めます。
問題では、図に示されている小数点の位置から、仮数部の最上位桁は小数点第一位であると判断します。
2進数0.01を最上位桁が小数点第一位になるように変形します。
$$ 0.01(2) = 0.1(2) \times 2 ^ {-1}$$
よって仮数部は1、指数部はー1になります。
つまり、 仮数部fは、10000000000 になります。
正規化の第2ステップとして、指数部を変形します。
問題には、指数部は「2を基数として、負数は2の補数で表現する」とあります。
1を4ビットで表現すると、0001です。
ビットを反転すると、1110です。
1を足すと、1111です。
よって、-1の2の補数は1111、つまり指数部eは1111となります。