B木やB⁺木がなぜ必要なのか良く分かっていなかったのが、下記のビデオで分かったので、まとめます。
B木(びーき)は、コンピュータサイエンスにおけるデータ構造、特に木構造の一つ。ブロック単位のランダムアクセスが可能な補助記憶装置(ハードディスクドライブなど)上に木構造を実装するのに適した構造として知られる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ハードディスクの構造
ハードディスクドライブ(英: hard disk drive, HDD)とは、磁性体を塗布した円盤を高速回転し、磁気ヘッドを移動することで、情報を記録し読み出す補助記憶装置の一種である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』

ハードディスクドライブは、音楽レコードプレーヤーに似ています。
レコード盤がディスク、レコードの針が磁気ヘッド、トーンアームはそのまま磁気ヘッドを搭載するアームです。
ディスクが回転して、アームが磁気ヘッドの位置を調整することで、ディスク上の任意の場所の情報を読み取ります。
トラック・セクター・ブロック・オフセット
ディスクセクタ(英: Disk sector)とは、伝統的に、ディスクドライブ(磁気ディスクや光ディスク)のトラック[1]の一部分を指す[2]。単にセクタとも呼ぶ。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ディスクは、トラックとセクターに分かれます。
上の図で言うと、ディスクの同心円状の部分をトラック(Aの部分)、扇形の部分を幾何学的セクター(Bの部分)と呼びます。
トラックとセクターにそれぞれ番号を振ることで、ディスク上の任意の場所を、トラックナンバーとセクターナンバーの組み合わせで表すことができます。
トラックとセクターが重なる部分、つまり、あるトラックナンバーとあるセクターナンバーで表される部分をブロック(トラックセクタ)(Cの部分)と呼びます。(通常は、このブロックのことを単にセクタと呼びます)
逆に言えば、1つのブロックは、トラックナンバーとセクターナンバーの組み合わせで表現できます。
余談ですが、複数のブロックを組み合わせるとクラスター(Dの部分)になります。
ブロックのサイズは、 ここでは、512バイトとすると、ブロックは以下のように表すことができます。
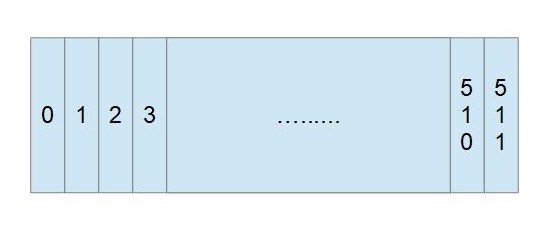
この一つ一つのまとまりをオフセットと呼びます。
つまり、ハードディスク上でデータにアクセスするためには、トラック、セクター、オフセットの番号が必要です。
メモリ階層
単純化すると、コンピュータは、CPUで利用する情報をハードディスクからメモリに読み込み、またメモリからハードディスクに書き込みます。
これはメモリー階層と呼ばれ、下の図のように表さ、下に行くほど読み込みが遅く、また容量が大きくなります。
CPUはメモリの情報を直接利用しますが、このCPU⇔メモリのデータの取扱いをどのようにして効率的に扱うかというのが、一般的なData Structure、データ構造の分野になります。
普通はデータ構造だけ考えれば十分なのですが、データベースのようハードディスクとのデータのやり取りも頻繁に発生する場合、CPU⇔メモリ⇔ハードディスクのデータの取扱いをどのようにして効率的に扱うかというところを考える必要が出てきます。
そこで、B木やB⁺木というアルゴリズムが出てきます。
データのインデックス
以下のような簡単なデータベースを考えます。
| id | 名前 | 会社 | メールアドレス | その他 |
|---|---|---|---|---|
| 1 | 鈴木 太郎 | 鈴木工業 | suzukitaro@example.com | あいうえお |
| 2 | 田中 次郎 | 田中商店 | tanakajiro@example.co.jp | かきくけこ |
| … | … | … | … | … |
| 100 | 山田 百郎 | 山田建設 | yamadahyakurou@example.ne.jp | ん |
テーブルの構造は、適当に以下のようになっていると考えます。
| id | 10バイト |
| 名前 | 30バイト |
| 会社 | 30バイト |
| メールアドレス | 30バイト |
| その他 | 28バイト |
| 合計 | 128バイト |
一つのレコードの合計は、128バイトです。
そうすると、512バイトのブロック(トラックセクタ)であれば、1つの ブロック(トラックセクタ) で、4つのレコードを保存することができます。
もし、レコードが100個あるとすると、データの保存には25ブロック (トラックセクタ) が必要になります。
このデータベースからidを用いて一つのレコードを検索することを考えると、どのブロックにそのデータが含まれるか分からないので、最悪の場合、25個全てのブロックにアクセスしなければなりません。
ブロックへのアクセスはハードディスクへのアクセスなので、時間がかかります。
そこでこのブロックへのアクセスを減らすため、インデックスを用います。
| id | そのレコードが含まれるブロックへのポインタ― |
| 1 | ブロック1番 |
| 2 | ブロック1番 |
| … | … |
| 100 | ブロック25番 |
上のようなインデックスを考えます。
idは10バイト、ポインタ―は適当に6バイト、一列の合計を16バイトとします。
このテーブルをハードディスク上に保存する場合、1 ブロック(トラックセクタ) には、32件のレコードを保存できるので、100件のレコードは4ブロックに収めることができます。
インデックスを加えることで、インデックスなしでは25のブロックへアクセスしなければならなかったのが、インデックスを4ブロック調べることで、そのデータへアクセスできるようになりました。
マルチレベルインデックス multilevel index
さらにデータベースが大きくなったとします。
| id | 名前 | 会社 | メールアドレス | その他 |
|---|---|---|---|---|
| 1 | 鈴木 太郎 | 鈴木工業 | suzukitaro@example.com | あいうえお |
| 2 | 田中 次郎 | 田中商店 | tanakajiro@example_shoten.com | かきくけこ |
| … | … | … | … | … |
| 100 | 山田 百郎 | 山田建設 | yamadahyakurou@example_kensetu.com | ん |
| … | … | … | … | … |
| 1000 | 安藤 千太郎 | 安藤商事 | andousentarou@example_shouji.com | abcdefg |
1000件のレコードを保存するので、250ブロック (トラックセクタ) 必要です。
インデックスはどうなるでしょうか?
| id | そのレコードが含まれるブロックへのポインタ― |
| 1 | ブロック1番 |
| 2 | ブロック1番 |
| … | … |
| 100 | ブロック25番 |
| … | … |
| 1000 | ブロック250番 |
インデックス一列の合計を16バイト、 1 ブロック(トラックセクタ) には32件のレコードを保存できたので、インデックスの保存には、32ブロック必要になり、もちろん検索は32ブロック全て行わなければならなくなります。
そこで、さらに、インデックスのインデックスを考えることができます。
下のようなインデックスのインデックスを考えます。
| id | そのレコードが含まれるインデックスへのポインタ― |
| 1 | インデックス1から32を含むブロックへのポインター |
| 33 | インデックス33から64を含むブロックへのポインター |
| … | |
| 992 | インデックス992から1023を含むブロックへのポインタ― |
同じように一列の合計は16バイトとします。
すると、1ブロックには32件のデータが保存できるので、上のインデックスのインデックスは、1ブロックに収めることができます。
よって、1ブロックを調べ、さらに1ブロックを調べれば、目的のデータへのアクセスができるようになります。
このように、ブロック (トラックセクタ) へのアクセスを減らすために、インデックスの多階層化を行うことを、マルチレベルインデックス multilevel indexと言います。
m-Way Search Tree
マルチインデックスは、左側が高レベルのインデックス、右側が低レベルのインデックスとして、 下の図のように考えることができます。
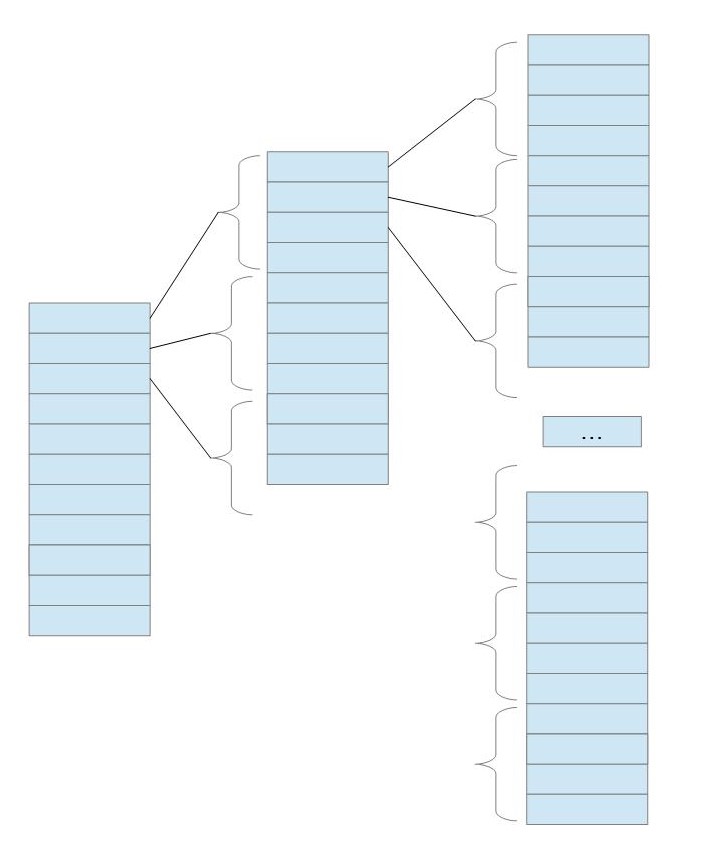
この図を右回転します。

木構造になっています。
この木構造は、2分探索木を拡張した、 m-way search tree により実現できます。
2分探索木とは 「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」 という制約を持つ、下のような木です。
2分探索木は、一つのノードの一つにキーを持ち、また一つのノードは2つの子を持ちます。
これを、一つのノードに複数のキーを持ち、また一つのノードに複数の子を持つように拡張します。
例えば、2-3木があります。
2-3木(-き)とは計算機科学におけるデータ構造で特に平衡木(balanced tree)に属する木構造の一種である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
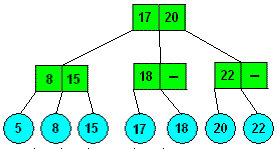
2-3木は、一つのノードに2つのキーを持ち、3つの子を持ちます。
このように、それぞれのノードが m 個の子、m-1 個のキーを持てるようにしたものを、m-way search tree と呼びます。
- それぞれのノードは、M個の子とM-1個のキーを持つ。
- それぞれのノードのキーは、昇順になっている。
- 最初のi番目の子供のキーは、i場面のキーより小さい。
- 最後のm-i番目の子供のキーは、i番目のキーより大きい。
2分探索木は2-way search tree、 2-3木は3-way search treeの一つです。
また、2-3-4木は、 4-way search treeの一つです。
2-3-4木(2-3-4き、英: 2-3-4 tree)または2-4木は計算機科学の用語であり、4次のB木(英: B-tree)と同じである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
4-way search treeのノードは、以下のように表すことができます。
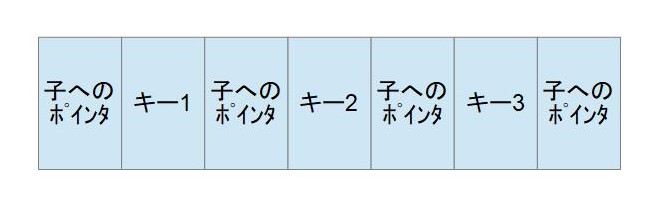
B木
しかし、m-way search tree のルールでは、例えば、10、20、30、40…というノードを挿入する際に、10の子として20、20の子として30、30の子として40…というような、線形の探索時間が必要になる挿入を行うことが可能になってしまいます。
そこで、AVL木やRed Black Treeのように、自動的に調整を行う仕組みを加えます。
これが B-tree です。
具体的には、以下の条件を満たすm-way search tree を、B-tree of order m と呼びます。
- 根は、唯一のノードでない限り、少なくとも2つの子を持つ。
- ルートでも葉でもないそれぞれのノードは、少なくともm/2個の空でない子供か、多くともm個の空でない子を持つ。
- ルートでも葉でもないそれぞれのノードのキーの数は、その空でない子供の数より一つ小さい。
- 全ての葉は同じ階層にある。
B木のノードの挿入
ノードの挿入は、ボトムアップ的に行われます。
検索の処理を行うことで、挿入しようとする値が木のどこに位置するべきかがわかる。まだ登録されていない値を検索した場合、処理は必ず葉ノードまで達する。すなわち、挿入処理は常に葉ノードを対象として開始される。ノードにまだ新たなキーを登録する余地がある場合、キーを追加して挿入処理は終了する。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
問題は、対象となるノードが既に許容できる最大数のキーを持っている場合である。この場合、ノードの分割処理を行う。分割が必要なノードからキーをひとつ選択し(通常、大小順で中央の値を選択する)、このキーより小さいキーだけを含むノードと、より大きいキーだけを含むノードに分割する。分割の基準となったキーは、親のノードに移動する。
ここで、親ノードに対してキーを追加している。親ノードでキーの最大数を越えた場合は、根に向かって順に分割処理を適用していく。根まで到達して根が分割された場合は、木の高さが1段増加することになる。分割直後の新しい根は、キーを1個と枝を2個だけ持っている。
例えば、 B-tree of order 4 に、10、20、40、50を挿入することを考えます。
10、20、40は普通に挿入して、3つのキーを持つノードになります。

ここに50のノードを挿入したいのですが、キーが3つを超えてしまうので、このままではできません。
そこで現在のノードの分割を行います。
分割が必要なノードからキーをひとつ選択する(通常、大小順で中央の値を選択する)。 (ここでは、20か40のどちらかが該当しますが、20にします)
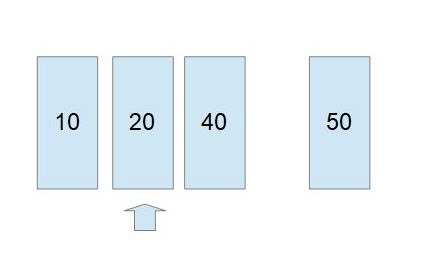
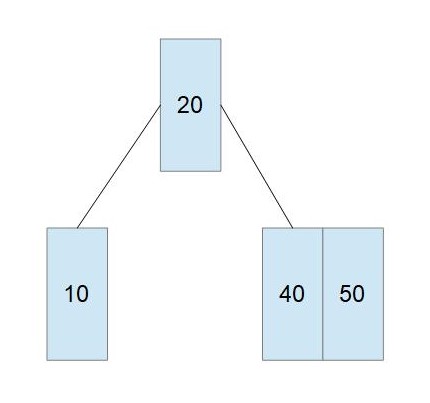
このキーより小さいキーだけを含むノードと、より大きいキーだけを含むノードに分割する。 分割の基準となったキーは、親のノードに移動する。
データベースにおいて、B-tree of order 4 のそれぞれのノードは、以下のように表すことができます。

B+木
B+木は、葉ノードにのみデータを格納するB木です。
B+木の葉ノードは、連結リストで相互にリンクすることで、連続したデータの検索が、B木より速くできるようになります。
B木のメリット
- B木は全てのノードがキーを持つので、検索の途中で目標にヒットする場合は、B+木より高速です。
B+木のメリット
- 葉を連結リストで繋げた場合、範囲検索に強いです。
- 葉のみがレコードへのポインタを持つため、 ブロック (トラックセクタ) の制限を考えた場合、途中のノードが多くのインデックスへのポインタを持つことができるので、階層をB木より低くなりインデックスへの検索がより早くなります。
