ヒープは過去にもまとめています。
最初よく混乱しますが、メモリのヒープとデータ構造のヒープは別のものです。
2分ヒープ
二分ヒープ(にぶんヒープ,バイナリヒープ,Binary heap)とは、二分木を使って作られるヒープ(データ構造)の特に単純な種類のひとつである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
2分ヒープは、2つの子を持つ木構造である2分木を使って作られ、要素の中で最大のもの(または最小のもの)がルートに来るように構成されるデータ構造です。
要素の中で最大のものがルートになる場合は max heap、最小のものがルートになる場合は min heap と呼ばれます。
2分ヒープを使うことで、要素の取得が\( O (1)\)で行える優先度付きキューを実装できます。
また、グラフの経路問題を解くダイクストラ法やプリム法にも使われます。
Heap Properties 2分ヒープの特性
赤黒木が守らなければならない Red Black Properties というルールがあったように、ヒープにも守らなければならない Heap Properties 2分ヒープの特性 があります。
完全2分木
ヒープの2分木は、完全2分木 ‘complete binary tree’ になっていなければなりません。
完全2分木 ‘complete binary tree’ とは、最下層以外はノードが全て埋まっており、また最下層のノードがある場合は、可能な限り左側に寄っている2分木です。
もしデータの挿入をする時は、次の空いている場所に挿入します。
親が子より常に大きい、又は常に小さい
max heap であれば「親が子より常に大きい」、min heap であれば「親が子より常に小さい」 という制約を満たします。
2分探索木のように 「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」というような制約はありません。
結果として、max heap であればルートが最大、min heap であればルートが最小になり、最大値や最小値の取得を\( O (1)\) で行うことができます。
ヒープと配列
max heap で考えます。
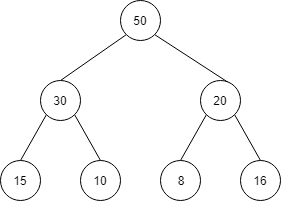
この max heap は、ルート→左の子→右の子→左の左の子→…という順で全てのノードにインデックスを振ることで、以下のような配列になります。
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 値 | 50 | 30 | 20 | 15 | 10 | 8 | 16 |
つまり、ヒープは一次元の配列で構成されます。
また、インデックス i のノードがあるとして、その子ノード、親ノードのインデックスは以下のようになります。
- そのノードの左側の子のインデックスは 2 * i + 1
- そのノードの右側の子のインデックスは 2 * i + 2
- そのノードの親のインデックスは i / 2 (切り下げ)
ヒープの操作
データの挿入
データの挿入が行われると、そのデータは最下層の空いている中で一番左側に挿入され、Heap Properties が維持されているかの確認が行い、必要であればデータを入れ替えます。
このヒープ構造の維持のためのデータの入れ替えを heapify と呼び、データの挿入はボトムアップ的に行われるので、heapify-up と呼ばれます。
以下のような max heap を考えます。
このヒープに15を挿入します。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 11 | 5 | 8 | 3 | 4 | 15 |
15は親の8より大きいので入れ替えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 11 | 5 | 15 | 3 | 4 | 8 |
さらに、15は親の11より大きいので入れ替えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 15 | 5 | 11 | 3 | 4 | 8 |
挿入が終わりました。
この操作は最悪木の高さだけ行われるので \( O (\log N) \) の計算量になります。
ヒープの構築
ヒープの構築は、配列に値を挿入する操作と、挿入した値が Heap Properties を維持できない場合に入れ替える Heapify の操作で行われます。
計算量は配列への挿入は\( O (N) \) 、Heapify は\( O (\log (N) \) で、\( O (N) + O (\log (N) = O (N) \) になります。
データのルートからの削除
ヒープからのデータの削除とは、通常はルートからの削除(つまり最大値/最小値の取り出し)を考えます。
ルートが削除されると、一番最後の要素をルートに持ってきて、その後 Heap Properties を維持するように値の入れ替えを行います。
一番最後の要素へのアクセスは、配列の一番最後の要素にインデックスでアクセスすれば良いので、\( O (1)\)で行えます。
この heapify はトップダウン的に行われるので heapify-down と呼ばれます。
以下のような max heap を考えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 11 | 5 | 8 | 3 | 4 |
11を削除すると、一番最後の4と入れ替えます。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 4 | 5 | 8 | 3 |
5 は Heap Properties を満たしますが、8は満たさないので、値の入れ替えを行います。
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 値 | 8 | 5 | 4 | 3 |
この操作は最悪木の高さだけ行われるので \( O (\log N) \) の計算量になります。
任意の箇所のデータの削除
通常は考えませんが、もしヒープで任意の箇所の値の削除を行う場合は、まず配列上で削除する値を探し削除し、その後ヒープを再構築します。
計算量は、配列での値の削除は\( O (N) \) 、Heapify は\( O (\log N) \) で、\( O (N) + O (\log N) = O (N) \) になります。
ヒープソート
ヒープソート (heap sort) とはリストの並べ替えを二分ヒープ木を用いて行うソートのアルゴリズムである[2](ヒープ領域とは無関係であることに注意する)。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ヒープソートは、探索によって最小値/最大値を探しソートするのではなく、ヒープのデータ構造を利用して最大値/最小値を探しソートします。
最悪で計算量が \( O ( N \log N) \)であり、クイックソートは最悪では\( O (N^2) \) になるので、最悪を考えた場合はクイックソートより良くなります。
最大値/最小値を先頭から取得したら、その要素を配列の一番最後の要素と交換し、ヒープからはその要素を削除します。
こうすると、配列上は存在しますが、ヒープ上は存在しない要素になります。
この操作を続けると、最終的にヒープから要素はなくなり配列上にはソートされた順序で要素が並ぶことになります。
ソートを行うために、追加的なメモリを必要としません。
ソートするためにまずヒープを構築しなければならないので、最初に\( O ( N) \) の計算量が必要になります。
ヒープの計算量
空間計算量は、\( N\)個の要素を保存するので \( O (N)\) になります。
最大値/最小値の探索は、配列の一番最初の値を探すだけなので\( O(1)\) で行えます。
値の挿入は、配列の一番最後への挿入が\( O(1) \) 、その後 heapify の操作が木の高さだけ行われ O(logN) の計算量になります。
削除も同様に、値の削除は \( O(1) \) ですが、その後 heapify の操作が木の高さだけ行われ O(logN) の計算量になります。
2分探索木では最大値/最小値の取得は、一番右端/左端の要素に移動するため\( O (\log N )\) の計算量になりましたが、ヒープは最大値/最小値の取得 が \( O(1)\)で行うことができるので、最大値/最小値の取得が必要なアルゴリズムでは、ヒープは有効な選択肢になります。
その他のヒープ構造
2項ヒープ
二項ヒープ(にこうヒープ、binomial heap)とは、計算機科学におけるデータ構造(ヒープ)の1つである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
2分ヒープは2分木を使いましたが、2項ヒープは 「2項木の集合」を使い、2つのヒープのマージを\( O ( \log N) \) で行うことができます。
フィボナッチヒープ
フィボナッチヒープ(英: Fibonacci heap)とは、計算機科学におけるデータ構造(ヒープ)の1つ。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
2分ヒープより高速ですが実装が難しいです。2項ヒープとおなじようにマージの操作を持つヒープで、特に値の追加を\( O (1) \) で行うことができます。



