プリム法を用いて、重み付き無向グラフの最小全域木を求めます。
プリム法はダイクストラ法とほぼ同じで、コードもダイクストラ法のものをほぼ流用しています。
全域木
全域木とは、グラフの中の全ての頂点を使って作られる木のことです。
全域木(ぜんいきぎ、英: Spanning tree)、極大木(きょくだいき)、スパニング木、スパニングツリーとは、グラフ理論において、以下のように定義される木のことである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
グラフ G(V,E) において T ⊆ E となる辺集合 T があるとき、グラフ S(V,T) が木(閉路を持たないグラフ)であるなら、 S(V,T) のことをグラフ G(V,E) の全域木であるとする。
つまり、あるグラフの全ての頂点とそのグラフを構成する辺の一部分のみで構成される木のことである。
最小全域木問題とは、グラフの各辺が重みをもつ場合、全ての辺の和が最小になる全域木を探し出す問題です。
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
From Wikipedia, the free encyclopedia
プリム法
プリム法とは、グラフ理論で重み付き連結グラフの最小全域木を求める最適化問題のアルゴリズムである。全域木(対象となるグラフの全頂点を含む辺の部分集合で構成される木)のうち、その辺群の重みの総和が最小となる木を求めるものである。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
以下の Wikipedia に載っているグラフの探索を行います。
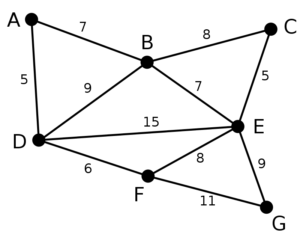
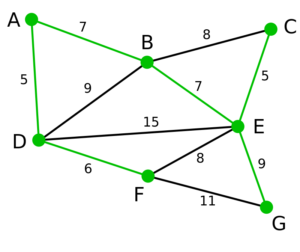
探索の結果、以下の緑線の最小全域木が求まり、重さの総和は39になります。
import heapq
import sys
class Vertex(object):
def __init__(self, id):
self.id = id
self.adjacent = {}
self.distance = sys.maxsize
self.visited = False
self.previous = None
def __lt__(self, other):
return self.distance < other.distance
def add_neighbor(self, neighbor, weight=0):
self.adjacent[neighbor] = weight
def get_neighbors(self):
return self.adjacent
def get_connections(self):
return self.adjacent.keys()
def get_vertex_id(self):
return self.id
def get_weight(self, neighbor):
return self.adjacent[neighbor]
def set_distance(self, distance):
self.distance = distance
def get_distance(self):
return self.distance
def set_previous(self, previous_vertex):
self.previous = previous_vertex
def get_previous(self):
return self.previous
def set_visited(self):
self.visited= True
class Graph(object):
def __init__(self):
self.vertex_dict = {}
self.num_vertex = 0
def __iter__(self):
return iter(self.vertex_dict.values())
def __len__(self):
return self.num_vertex
def add_vertex(self, id):
self.num_vertex = self.num_vertex + 1
new_vertex = Vertex(id)
self.vertex_dict[id] = new_vertex
return new_vertex
def get_vertex(self, id):
if id in self.vertex_dict:
return self.vertex_dict[id]
else:
return None
def add_edge(self, frm, to, weight=0):
if frm not in self.vertex_dict:
self.add_vertex(frm)
if to not in self.vertex_dict:
self.add_vertex(to)
self.vertex_dict[frm].add_neighbor(self.vertex_dict[to], weight)
# プリム法は無向グラフ
self.vertex_dict[to].add_neighbor(self.vertex_dict[frm], weight)
def get_vertices(self):
return self.vertex_dict.keys()
def get_edges(self):
edges = []
for v in self.vertex_dict.values():
for w in v.get_connections():
vid = v.get_vertex_id()
wid = w.get_vertex_id()
edges.append((vid, wid, v.get_weight(w)))
return edges
def prim(graph, source):
source.set_distance(0)
priority_queue = [(vertex.get_distance(), vertex) for vertex in graph]
heapq.heapify(priority_queue)
while len(priority_queue):
nearest_vrtex = heapq.heappop(priority_queue)
current = nearest_vrtex[1]
current.set_visited()
for next in current.adjacent:
if next.visited:
continue
new_distance = current.get_weight(next)
if next.get_distance() > new_distance:
next.set_distance(new_distance)
next.set_previous(current)
heapq.heapify(priority_queue)
total_distance = 0
for vertex in graph.vertex_dict.values():
if vertex.get_previous():
print(f'辺 {vertex.get_vertex_id()}{vertex.previous.get_vertex_id()} --> {vertex.get_distance()}')
total_distance += vertex.get_distance()
print(f'総距離 {total_distance}')
if __name__ == '__main__':
graph = Graph()
graph.add_vertex('a')
graph.add_vertex('b')
graph.add_vertex('c')
graph.add_vertex('d')
graph.add_vertex('e')
graph.add_vertex('f')
graph.add_vertex('g')
graph.add_edge('a', 'b', 7)
graph.add_edge('a', 'd', 5)
graph.add_edge('b', 'c', 8)
graph.add_edge('b', 'd', 9)
graph.add_edge('b', 'e', 7)
graph.add_edge('c', 'e', 5)
graph.add_edge('d', 'e', 15)
graph.add_edge('d', 'f', 6)
graph.add_edge('e', 'f', 8)
graph.add_edge('e', 'g', 9)
graph.add_edge('f', 'g', 11)
source = graph.get_vertex('d')
prim(graph, source)
# 辺 ad --> 5
# 辺 ba --> 7
# 辺 ce --> 5
# 辺 eb --> 7
# 辺 fd --> 6
# 辺 ge --> 9
# 総距離 39
想定通りの結果を得ることができました。
