スタック
スタックは、コンピュータで用いられる基本的なデータ構造の1つで、データを後入れ先出し(LIFO: Last In First Out; FILO: First In Last Out)の構造で保持するものである。抽象データ型としてのそれを指すこともあれば、その具象を指すこともある。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
stack は「積み重なったもの」というような意味です。
ADTとしてのスタックは、Pop Push Peek といった基本的な操作を持ち、一番最後に挿入したデータを一番最初に取り出す、 LIFO: Last In First Out 後入れ先出しの構造でデータを保持します。
配列、連結リスト、どちらのデータ構造を使っても簡単に実装することができます。
とても身近な例だと、webブラウザの戻るボタン(訪れたurlをスタックに積み上げておき、「戻る」際には一番上のurlを持ってくる)やアプリのundoボタン(操作を行う前の状態をスタックに積み上げておき、「undo」の際にはスタックの一番上の状態を持ってくる)でスタックは使われています。
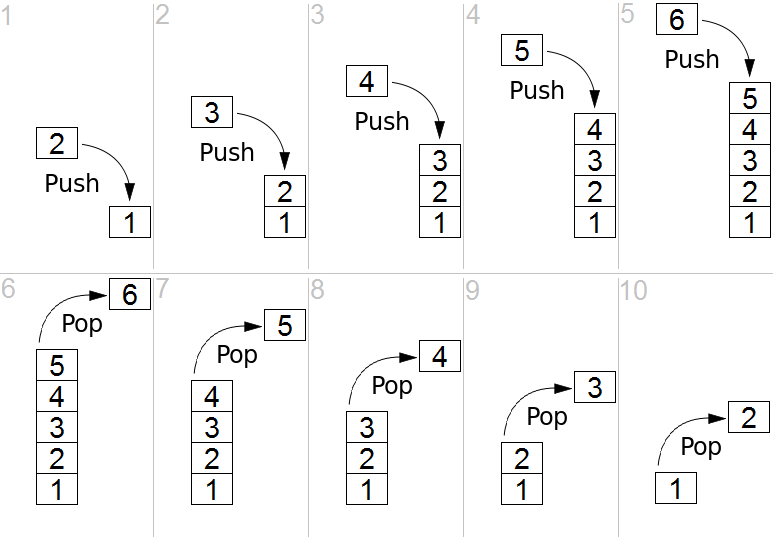
Push
Push は「押す」というような意味です。
しかしスタックのPush はちょっとイメージと異なり、スタックの上にデータを積み上げていく操作です。
\( O(1) \) で実行することができます。
Pop
Popは「ポンっと飛び出てくるイメージ」の単語です。
スタックでの Pop は、スタックの一番上のデータを取り出す操作です。
「一番上のデータ」とは「一番最後に積み上げたデータ」のことで、Push と Pop の操作で、LIFO: Last In First Out 後入れ先出し のデータ構になります。
\( O(1) \) で実行できます。
Peek
Peek は「のぞき見」です。
スタックでの Peek は、スタックの一番上のデータを確認する操作です。
Pop はデータを取り出すので、Pop することでスタックからそのデータは失われます。
Peek はデータを確認するだけなので、Peek してもデータは失われません。
\(O(1)\)で実行できます。
コールスタック
スタックの応用として、コールスタックを考えます。
コールスタック (Call Stack)は、プログラムで実行中のサブルーチンに関する情報を格納するスタックである。実行中のサブルーチンとは、呼び出されたが処理を完了していないサブルーチンを意味する。実行スタック (Execution Stack)、制御スタック (Control Stack)、関数スタック (Function Stack)などとも呼ばれる。また、単に「スタック」と言ったときにコールスタックを指していることが多い。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
プログラミング言語によって異なると思いますが、基本的には、メモリの確保を行う際に、スタックメモリとヒープメモリというようにメモリ領域を分けて考えます。
コールスタック/スタックメモリ
コールスタック/スタックメモリは、コンピュータのメモリ上の特殊な領域で、プログラムの中で、「現在実行しているサブルーチン(メソッド/関数)」を保持します。
コールスタックを使うことで、 「現在実行しているサブルーチン(メソッド/関数)」 が終了したら次に行う処理を、自動的にに把握することができます。
また、 「現在実行しているサブルーチン(メソッド/関数)」 でしか使わない局所変数を コールスタック/スタックメモリ に格納することで、メモリ領域の確保/解放が自動的に実行することができます。
通常、スタックメモリは決まった領域が確保されていて、その領域を超えるとスタックオーバーフローが起こってしまいます。
ヒープメモリ
ヒープメモリは、スタックメモリより広い領域を扱うことができ、 「現在実行しているサブルーチン(メソッド/関数)」 に制限されないメモリ領域ですが、ソフトウエア側で意識的に確保と解放を行わなければならないメモリ領域です。
もしメモリ解放を行わなかった場合、不必要なメモリが確保されたままになってしまうメモリリークが起こってしまいます。
ガベージコレクション という仕組みを用いることで、不要なヒープメモリの解放が自動的に行えるようになっている場合もあります。
ポインタを用いてアクセスするので、スタックより低速です。
スタックメモリとヒープメモリの比較
スタックメモリとヒープメモリの比較を簡単にまとめます。
| スタック | ヒープ |
|---|---|
| メモリ領域は限定 | メモリ領域は無制限 |
| アクセス速い | アクセス遅い |
| 局所変数 | オブジェクト等 |
| CPUが効率的にメモリ管理 | 手動でメモリ管理 |
スタックと再帰
スタックの応用として、再帰を考えます。
再帰を使うアルゴリズムを実行する時、実際のところ、OSはスタックを使って呼び出された関数をスタックに積み上げていき、上から順に処理していくことで実行しています。
つまり「再帰を使うアルゴリズム」は、「スタックを使うアルゴリズム」に変換することができます。
例えば、深さ優先探索の疑似コードは以下のようになり 、再帰を使ってもスタックを使っても同じ結果になるアルゴリズムを書くことができます。
再帰
# https://ja.wikipedia.org/wiki/%E6%B7%B1%E3%81%95%E5%84%AA%E5%85%88%E6%8E%A2%E7%B4%A2
function 深さ優先探索(v)
v に訪問済みの印を付ける
v を処理する
for each v に接続している頂点 i do
if i が未訪問 then
深さ優先探索(i)
スタック
# https://ja.wikipedia.org/wiki/%E6%B7%B1%E3%81%95%E5%84%AA%E5%85%88%E6%8E%A2%E7%B4%A2
function 深さ優先探索(v)
S ← 空のスタック
v に訪問済みの印を付ける
v を S に積む
while S が空ではない do
v ← S から取り出す
v を処理する
for each v に接続している頂点 i do
if i が未訪問 then
i に訪問済みの印を付ける
i を S に積む
階乗
具体的に再帰関数の動きを見るため、階乗の再帰関数を考えます。
階乗とは、\(n ! = n \times (n-1) \times … \times 2 \times 1 \) という計算です。
多くのプログラミング言語において、再帰的な定義を利用し、プロシージャの再帰呼び出しを用いた階乗の実装が可能である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
階乗は再帰関数を使って下のように書かれます。
int factorial(int n)
{
int x;
if (n == 0) {
x = 1; // 0! = 1
} else {
x = n * factorial(n - 1);
}
return x;
}
この関数は、ある整数\(n\)が与えられると、\(n = 0\) になるまで\(n\)を1ずつ減らしながら自分自身を呼び出し続けます。
これは同じ関数の連続した呼び出しであり、前述のコールスタックの仕組みを用いることで、呼び出される関数が終了条件に到達するまでスタックに積みあがっていくことで実現されます。
よって、スタックメモリのメモリ上限内に終了条件に到達できない場合は、スタックオーバーフローが起こります。
factorial(3) の実行を考えます。
| factorial(3) |
\(n = 0\)でないので、3 * factorial(2) が呼び出されます。
| 3 * factorial(2) |
| factorial(3) |
まだ \(n = 0\)でないので、2 * factorial(1) が呼び出されます。
| 2 * factorial(1) |
| 3 * factorial(2) |
| factorial(3) |
\(n = 0\) になり、1 が返されます。
| return 1 |
| 2 * factorial(1) |
| 3 * factorial(2) |
| factorial(3) |
よって、あとは次々に代入が進み、計算が実行されます。
| return 2 * 1 |
| 3 * factorial(2) |
| factorial(3) |
| return 3 * 2 * 1 |
| factorial(3) |
最終的に、\( 3 \times 2 \times 1 \) が返ってきます。
Python でスタックを実装
Python でリストを用いて最低限のスタックを実装してみます。
「Python のリスト」は配列とほぼ同じと考えることができ、push pop peek とも\( O (1) \) になります。
class Stack(object):
def __init__(self):
self.stack = []
# O(1)
def push(self, data):
self.stack.append(data)
# O(1)
def pop(self):
data = self.stack[-1]
del self.stack[-1]
return data
# O(1)
def peek(self):
data = self.stack[-1]
return data
if __name__ == '__main__':
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
# 3
print('peeked', stack.peek())
print('popped', stack.pop())
# 2
print('peeked',stack.peek())
print('popped', stack.pop())
# 1
print('peeked', stack.peek())
print('popped', stack.pop())
# IndexError
print('peeked', stack.peek())
print('popped', stack.pop())
実際は、Python でスタックを使いたい時は、特にclass を定義する必要はなく、リストのそのままで実現できます。

