幅優先探索
幅優先探索(はばゆうせんたんさく、英: breadth first search)はグラフ理論(Graph theory)において木構造(tree structure)やグラフ(graph)の探索に用いられるアルゴリズム。アルゴリズムは根ノードで始まり隣接した全てのノードを探索する。それからこれらの最も近いノードのそれぞれに対して同様のことを繰り返して探索対象ノードをみつける。「横型探索」とも言われる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
幅優先探索を行うことで、グラフの全てのノードを一度だけ訪れることができます。
開始ノードの隣接したノード全てを訪れてから、さらにその隣接ノードと隣接したノード全てを訪れる、ということを、全てノードが訪問済みになるまで繰り返します。
\(|E|\)をグラフ内の辺の数として、最悪の場合幅優先探索は全ての辺を考慮するので、時間計算量は\(O(|E|)\)になります。
\(|V|\)をグラフ内の頂点の数として、幅優先探索は全ての頂点を考慮するので、空間計算量は\(O(|V|)\)になります。
最悪の空間計算量は、幅優先探索、深さ優先探索とも変わりませんが、一般的には深さ優先探索の方が小さいので、深さ優先探索の方が良いとされます。
ただし、ダイクストラ法のように、幅優先探索を使うアルゴリズムもあります。
疑似コード
幅優先探索はFIFOのADTであるキューを使います。
キューから現在の頂点を取り出し、隣接する頂点が訪問済みかどうかを確認し、訪問していない場合はキューに入れます。これをキューが空になるまで繰り返します。
function 幅優先探索(v)
Q ← 空のキュー
v に訪問済みの印を付ける
v を Q に追加
while Q が空ではない do
v ← Q から取り出す
v を処理する
for each v に接続している頂点 i do
if i が未訪問 then
i に訪問済みの印を付ける
i を Q に追加
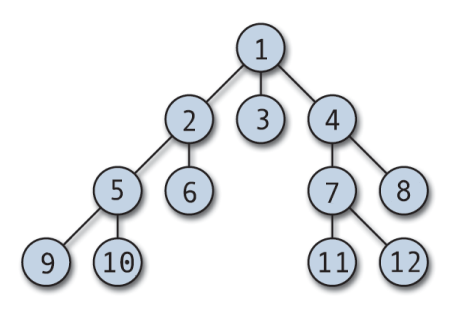
例えば、以下のようなグラフを考えて、1からスタートするとします。
まずは、1をキューに入れてから1を取り出し、次に1と隣接する2、3、4をキューに入れます。この状態では、キューは2,3,4を持ちます。
次にキューから2を取り出し、2と隣接し訪問済みではない5,6をキューに入れます。この状態ではキューは3,4,5,6を持ちます。
この処理を、全てのノードが訪問済みになるまで、つまりキューが空になるまで繰り返すことで、全てのノードを訪れることができます。
幅優先探索の応用例
対戦型ソフト
思考時間に制限があるような場合は、深さ優先探索(DFS)だと偏った候補手しか読めないので時間に追われて悪手を選ぶことがあるが、幅優先探索(BFS)を使えばいつ読みを中断されてもそれなりに有効な一手を選ぶことが出来る。
序盤はBFSを使って広く浅く読み、終盤はDFSを使ってゲームの終局(詰み)まで読み切るように作れば強いソフトが作れる
幅優先探索(BFS)で対戦型ソフトを強くできるのか?
最初は幅優先探索、注目するところは深さ優先探索を使い認識すると人間らしくなりそうです。
Cheney’s algorithm
Cheney’s algorithm, first described in a 1970 ACM paper by C.J. Cheney, is a stop and copy method of tracing garbage collection in computer software systems.
From Wikipedia, the free encyclopedia
エドモンズ・カープのアルゴリズム
エドモンズ・カープのアルゴリズム(英: Edmonds-Karp algorithm)は、フローネットワークの最大フロー問題を解くフォード・ファルカーソンのアルゴリズムの実装の一種であり、\(O(VE^2)\) の計算量である 。
出典: フリー百科事典『ウィキペディア(Wikipedia)』