Python で重み無しの有向グラフの単一始点最短経路問題を解きます。
以下の続きです。
DFSを使ったトポロジカルソートを Python で書きます。
以下の続きです。
深さ優先探索トポロジカルソート
トポロジカルソートの別のアルゴリズムは深さ優先探索をベースにしている。このアルゴリズムではグラフの各ノードについて、トポロジカルソ...
yottagin.com
2019-08-16 15:38
最短経路問題
グラフ理論における最短経路問題（さいたんけいろもんだい、英: shortest path problem）とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。
出典: フリー百科事典『ウィキペディア（Wikipedia）』
辺の重みのない有向グラフの単一始点からの最短経路問題は、幅優先探索を使って解くことができます。
無向グラフの幅優先探索は、以下で扱っています。
無向グラフをBFSで探索するアルゴリズムを Python で記述します。
以下の続きです。
幅優先探索
幅優先探索（はばゆうせんたんさく、英: breadth first search）はグラフ理論(Graph theory)において木構造(...
yottagin.com
2019-08-14 15:32
有向グラフでは、スタート地点からの距離と移動前の点をそれぞれの点が属性として持ち、幅優先探索の際にこの属性を更新していくことで、最終的に最短経路を得ることができます。
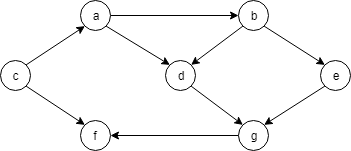
以下のようなグラフを探索します。
import collections
class Vertex(object):
def __init__(self, id):
self.id = id
self.adjacent = {}
# 開始点からの距離
self.distance = -1
# 前の点を記録し、最短経路を出力する時に使う
self.previous = None
def add_neighbor(self, neighbor, weight=0):
self.adjacent[neighbor] = weight
def get_neighbors(self):
return self.adjacent
def get_connections(self):
return self.adjacent.keys()
def get_vertex_id(self):
return self.id
def get_weight(self, neighbor):
return self.adjacent[neighbor]
def set_distance(self, distance):
self.distance = distance
def get_distance(self):
return self.distance
def set_previous(self, previous_vertex):
self.previous = previous_vertex
def get_previous(self):
return self.previous
class Graph(object):
def __init__(self):
self.vertex_dict = {}
self.num_vertex = 0
def __iter__(self):
return iter(self.vertex_dict.values())
def add_vertex(self, id):
self.num_vertex = self.num_vertex + 1
new_vertex = Vertex(id)
self.vertex_dict[id] = new_vertex
return new_vertex
def get_vertex(self, id):
if id in self.vertex_dict:
return self.vertex_dict[id]
else:
return None
def add_edge(self, frm, to, weight=0):
if frm not in self.vertex_dict:
self.add_vertex(frm)
if to not in self.vertex_dict:
self.add_vertex(to)
self.vertex_dict[frm].add_neighbor(self.vertex_dict[to], weight)
def get_vertices(self):
return self.vertex_dict.keys()
def get_edges(self):
edges = []
for v in self.vertex_dict.values():
for w in v.get_connections():
vid = v.get_vertex_id()
wid = w.get_vertex_id()
edges.append((vid, wid, v.get_weight(w)))
return edges
def solve_shortest_path_unweighted_graph(graph, start):
start = graph.get_vertex(start)
start.set_distance(0)
start.set_previous(None)
queue = collections.deque()
queue.append(start)
while queue:
current_vertex = queue.popleft()
for neighbor in current_vertex.get_connections():
if neighbor.get_distance() == -1:
neighbor.set_distance(current_vertex.get_distance() + 1)
neighbor.set_previous(current_vertex)
queue.append(neighbor)
for vertex in graph.vertex_dict.values():
if vertex.get_distance() == -1:
print(f'{start.get_vertex_id()} から {vertex.get_vertex_id()} へは移動できません。')
continue
elif vertex.get_distance() == 0:
continue
else:
print(f'{start.get_vertex_id()} から {vertex.get_vertex_id()} の最短距離は {vertex.get_distance()}。', end='')
# 最短経路の出力
if vertex.get_distance()>0:
route = [vertex.get_vertex_id()]
current_vertex = vertex
while current_vertex.get_previous():
route.append(current_vertex.get_previous().get_vertex_id())
current_vertex = current_vertex.get_previous()
print('移動ルート', route[::-1])
if __name__ == '__main__':
graph = Graph()
graph.add_vertex('a')
graph.add_vertex('b')
graph.add_vertex('c')
graph.add_vertex('d')
graph.add_vertex('e')
graph.add_vertex('f')
graph.add_vertex('g')
graph.add_edge('a', 'b', 1)
graph.add_edge('a', 'd', 1)
graph.add_edge('b', 'd', 1)
graph.add_edge('b', 'e', 1)
graph.add_edge('c', 'a', 1)
graph.add_edge('c', 'f', 1)
graph.add_edge('d', 'g', 1)
graph.add_edge('e', 'g', 1)
graph.add_edge('g', 'f', 1)
solve_shortest_path_unweighted_graph(graph, 'a')
# a から b の最短距離は 1。移動ルート ['a', 'b']
# a から c へは移動できません。
# a から d の最短距離は 1。移動ルート ['a', 'd']
# a から e の最短距離は 2。移動ルート ['a', 'b', 'e']
# a から f の最短距離は 3。移動ルート ['a', 'd', 'g', 'f']
# a から g の最短距離は 2。移動ルート ['a', 'd', 'g']
想定通りの結果を得ることができました。