トポロジカルソートを Python で書きます。
以下の続きです。
無向グラフをBFSで探索するアルゴリズムを Python で記述します。
以下の続きです。
幅優先探索
幅優先探索（はばゆうせんたんさく、英: breadth first search）はグラフ理論(Graph theory)において木構造(...
yottagin.com
2019-08-14 15:32
トポロジカルソート
トポロジカルソート（英: topological sort）とは、グラフ理論において、有向非巡回グラフ（英: directed acyclic graph, DAG）の各ノードを順序付けして、どのノードもその出力辺の先のノードより前にくるように並べることである。有向非巡回グラフは必ずトポロジカルソートすることができる。
出典: フリー百科事典『ウィキペディア（Wikipedia）』
トポロジカルソートは、例えば、a, b, cというタスクがあって、a, b が終わってから c に取り掛かれるような時に、[a, b] -> [c] というような順序に要素を並び替えるソートです。
こういったタスクの依存関係はDAGを使って表すことができるので、DAGの問題として取り扱うことができます。
Kahn’s algorithm
Kahn (1962)[2] が発明したアルゴリズムは、トポロジカルソートされた結果になるようにノードを順に選択していくというものである。
出典: フリー百科事典『ウィキペディア（Wikipedia）』
のアルゴリズムで書きます。
幅優先探索のように行います。
「入力辺を持たないノード」を開始ノードにして、「入力辺を持たないノード」から隣接ノードへのエッジを削除します。
もし隣接ノードが削除したノード以外に入力エッジを持たない場合は、この隣接ノードは開始ノードに続くノードと判断できます。
def topological_sort_bfs(graph):
# トポロジカルソートした結果を蓄積する空リスト
topological_sorted_list = []
queue = collections.deque()
# 入力辺を持たないすべてのノードの集合
for vertex in graph:
indegree = vertex.get_indegree()
if indegree == 0:
queue.append(vertex)
# while S が空ではない do
while len(queue) > 0:
# S からノード n を削除する
current_vertex = queue.popleft()
# L に n を追加する
topological_sorted_list.append(current_vertex.get_vertex_id())
# for each n の出力辺 e とその先のノード m do
for neighbor in current_vertex.get_connections():
# 辺 e をグラフから削除する
neighbor.set_indegree(neighbor.get_indegree() - 1)
# if m がその他の入力辺を持っていなければ then
if neighbor.get_indegree() == 0:
# m を S に追加する
queue.append(neighbor)
if len(topological_sorted_list) != len(graph.get_vertices()):
print("Kahn's algorithm:", '閉路があります。DAGではありません。')
else:
print("Kahn's algorithm tological sorted list:", topological_sorted_list)
深さ優先探索トポロジカルソート
幅優先探索のように行えるということは、深さ優先探索のように行うこともできます。
トポロジカルソートの別のアルゴリズムは深さ優先探索をベースにしている。このアルゴリズムではグラフの各ノードについて、トポロジカルソートを始めてからすでに訪れたノードに到達するまで深さ優先探索を行う
出典: フリー百科事典『ウィキペディア（Wikipedia）』
深さ優先探索中に訪れたノードには全て 「一時的」というマークを付け、もしその後の深さ優先探索で再度 「一時的」 のマークの付いたノードに出会った場合は、その部分は閉路になっていると判断できます。
また、リストへの追加を先頭ではなく、append で後方に行っているため、リストを読みだすときは逆順で行っています。
def topological_sort_dfs(graph):
# L ← トポロジカルソートされた結果の入る空の連結リスト
topological_reverse_sorted_list = []
try:
# for each ノード n do
for current_vertex in graph:
# if n に permanent の印が付いていない then
if not(current_vertex.permanent):
topological_sort_dfs_visit(current_vertex, topological_reverse_sorted_list)
# 閉路を発見した場合
except GraphTopologicalError:
print('DFS algorithm:', '閉路があります。DAGではありません。')
else:
# リストは最後から読み出す
print("DFS algorithm tological sorted list:", topological_reverse_sorted_list[::-1])
def topological_sort_dfs_visit(vertex, topological_sorted_list):
if vertex.permanent:
return
# if n に「一時的」の印が付いている then
if vertex.temporary:
# 閉路があり DAG でないので中断
raise GraphTopologicalError(topological_sorted_list)
# n に「一時的」の印を付ける
vertex.temporary = True
# for each n の出力辺 e とその先のノード m do
for neighbor in vertex.get_connections():
topological_sort_dfs_visit(neighbor, topological_sorted_list)
vertex.temprary = False
# n に「恒久的」の印を付ける
vertex.permanent = True
# n を L に追加
topological_sorted_list.append(vertex.get_vertex_id())
テスト
以下の2つのグラフでトポロジカルソートを行います。
最初のグラフはDAGなので、[a, b, c, d, e] （または [a, c, b, d, e] ）と出力してくれれば問題ありません。
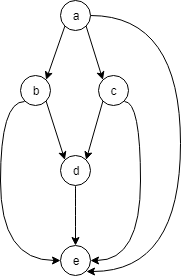
次のグラフは、e から a へと巡回してしまっているので、「DAGではありません」と出力します。
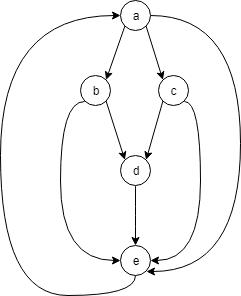
import collections
class Vertex(object):
def __init__(self, id):
self.id = id
self.adjacent = {}
self.visited = False
# 入力辺のカウント
self.in_degree = 0
# DFSトポロジカルソートで使うマーク
self.permanent = False
self.temporary = False
def add_neighbor(self, neighbor, weight=0):
self.adjacent[neighbor] = weight
def get_neighbors(self):
return self.adjacent
def get_connections(self):
return self.adjacent.keys()
def get_vertex_id(self):
return self.id
def get_weight(self, neighbor):
return self.adjacent[neighbor]
def set_visited(self):
self.visited = True
def unset_visited(self):
self.visited = False
def set_indegree(self, num):
self.in_degree = num
def get_indegree(self):
return self.in_degree
class Graph(object):
def __init__(self):
self.vertex_dict = {}
self.num_vertex = 0
def __iter__(self):
return iter(self.vertex_dict.values())
def add_vertex(self, id):
self.num_vertex = self.num_vertex + 1
new_vertex = Vertex(id)
self.vertex_dict[id] = new_vertex
return new_vertex
def get_vertex(self, id):
if id in self.vertex_dict:
return self.vertex_dict[id]
else:
return None
def add_edge(self, frm, to, weight=0):
if frm not in self.vertex_dict:
self.add_vertex(frm)
if to not in self.vertex_dict:
self.add_vertex(to)
self.vertex_dict[frm].add_neighbor(self.vertex_dict[to], weight)
# 入力辺を増やす
self.vertex_dict[to].in_degree += 1
def get_vertices(self):
return self.vertex_dict.keys()
def get_edges(self):
edges = []
for v in self.vertex_dict.values():
for w in v.get_connections():
vid = v.get_vertex_id()
wid = w.get_vertex_id()
edges.append((vid, wid, v.get_weight(w)))
return edges
class GraphTopologicalError(Exception):
pass
def topological_sort_bfs(graph):
# トポロジカルソートした結果を蓄積する空リスト
topological_sorted_list = []
queue = collections.deque()
# 入力辺を持たないすべてのノードの集合
for vertex in graph:
indegree = vertex.get_indegree()
if indegree == 0:
queue.append(vertex)
# while S が空ではない do
while len(queue) > 0:
# S からノード n を削除する
current_vertex = queue.popleft()
# L に n を追加する
topological_sorted_list.append(current_vertex.get_vertex_id())
# for each n の出力辺 e とその先のノード m do
for neighbor in current_vertex.get_connections():
# 辺 e をグラフから削除する
neighbor.set_indegree(neighbor.get_indegree() - 1)
# if m がその他の入力辺を持っていなければ then
if neighbor.get_indegree() == 0:
# m を S に追加する
queue.append(neighbor)
if len(topological_sorted_list) != len(graph.get_vertices()):
print("Kahn's algorithm:", '閉路があります。DAGではありません。')
else:
print("Kahn's algorithm tological sorted list:", topological_sorted_list)
def topological_sort_dfs(graph):
# L ← トポロジカルソートされた結果の入る空の連結リスト
topological_reverse_sorted_list = []
try:
# for each ノード n do
for current_vertex in graph:
# if n に permanent の印が付いていない then
if not(current_vertex.permanent):
topological_sort_dfs_visit(current_vertex, topological_reverse_sorted_list)
# 閉路を発見した場合
except GraphTopologicalError:
print('DFS algorithm:', '閉路があります。DAGではありません。')
else:
# リストは最後から読み出す
print("DFS algorithm tological sorted list:", topological_reverse_sorted_list[::-1])
def topological_sort_dfs_visit(vertex, topological_sorted_list):
if vertex.permanent:
return
# if n に「一時的」の印が付いている then
if vertex.temporary:
# 閉路があり DAG でないので中断
raise GraphTopologicalError(topological_sorted_list)
# n に「一時的」の印を付ける
vertex.temporary = True
# for each n の出力辺 e とその先のノード m do
for neighbor in vertex.get_connections():
topological_sort_dfs_visit(neighbor, topological_sorted_list)
vertex.temprary = False
# n に「恒久的」の印を付ける
vertex.permanent = True
# n を L に追加
topological_sorted_list.append(vertex.get_vertex_id())
if __name__ == '__main__':
graph = Graph()
graph.add_vertex('a')
graph.add_vertex('b')
graph.add_vertex('c')
graph.add_vertex('d')
graph.add_vertex('e')
graph.add_edge('a', 'b', 1)
graph.add_edge('a', 'c', 1)
graph.add_edge('a', 'e', 1)
graph.add_edge('b', 'd', 1)
graph.add_edge('b', 'e', 1)
graph.add_edge('c', 'd', 1)
graph.add_edge('c', 'e', 1)
graph.add_edge('d', 'e', 1)
topological_sort_bfs(graph)
# Kahn's algorithm tological sorted list: ['a', 'b', 'c', 'd', 'e']
topological_sort_dfs(graph)
# DFS algorithm tological sorted list: ['a', 'c', 'b', 'd', 'e']
graph = Graph()
graph.add_vertex('a')
graph.add_vertex('b')
graph.add_vertex('c')
graph.add_vertex('d')
graph.add_vertex('e')
graph.add_edge('a', 'b', 1)
graph.add_edge('a', 'c', 1)
graph.add_edge('a', 'e', 1)
graph.add_edge('b', 'd', 1)
graph.add_edge('b', 'e', 1)
graph.add_edge('c', 'd', 1)
graph.add_edge('c', 'e', 1)
graph.add_edge('d', 'e', 1)
graph.add_edge('e', 'a', 1)
topological_sort_bfs(graph)
# Kahn's algorithm: 閉路があります。DAGではありません。
topological_sort_dfs(graph)
# DFS algorithm: 閉路があります。DAGではありません。
想定通りの結果を得ることができました。