[グラフ] DAGの最短経路

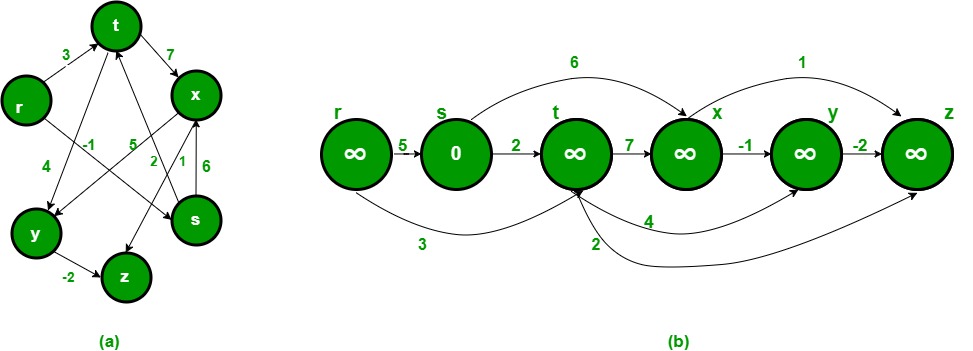
DAG

DAG とは Directed acyclic graph 有向非巡回グラフの略で、閉路のない有向グラフのことです。

有向非巡回グラフ、有向非循環グラフ、有向無閉路グラフ（ゆうこうひじゅんかいグラフ、英: Directed acyclic graph, DAG）とは、グラフ理論における閉路のない有向グラフのことである。有向グラフは頂点と有向辺（方向を示す矢印付きの辺）からなり、辺は頂点同士をつなぐが、ある頂点 \(v\) から出発し、辺をたどり、頂点 \(v\) に戻ってこないのが有向非巡回グラフである^[1][2][3]。
出典: フリー百科事典『ウィキペディア（Wikipedia）』

DAG であれば、トポロジカルソートを使うことで、ダイクストラ法やベルマンフォード法より速く、\( O(V + E)\)で最短経路を求めることができます。

トポロジカルソート

トポロジカルソート（英: topological sort）とは、グラフ理論において、有向非巡回グラフ（英: directed acyclic graph, DAG）の各ノードを順序付けして、どのノードもその出力辺の先のノードより前にくるように並べることである。有向非巡回グラフは必ずトポロジカルソートすることができる。
出典: フリー百科事典『ウィキペディア（Wikipedia）』

DAGでなので、「入力辺を持たないノード」は開始ノードになります。

「入力辺を持たないノード」から隣接ノードへのエッジを削除します。

もし隣接ノードが他に入力エッジを持たない場合は、この隣接ノードは開始ノードに続くノードと判断できます。

トポロジカルソートの計算量は\(O(V+E)\)です。

以下のグラフ (a) をトポロジカルソートしてみます。

import collections
import sys


class Node(object):

    def __init__(self, name):
        self.name = name
        self.indegree = 0
        self.adjacency_list = []
        self.predecessor = None
        

class ShortestPathDAG(object):

    def __init__(self, nodes):
        self.nodes = nodes
        self.topological_sorted_list = []

    def topological_sort(self):

        queue = collections.deque()

        for node in self.nodes:
            if node.indegree == 0:
                queue.append(node)

        while queue:
            current_node = queue.popleft()
            self.topological_sorted_list.append(current_node)
            for neighbor, weight in current_node.adjacency_list:
                neighbor.indegree -= 1
                if neighbor.indegree == 0:
                    queue.append(neighbor)

        if len(self.nodes) != len(self.topological_sorted_list):
            raise Exception('Not DAG')


if __name__ == '__main__':
    r = Node('r')
    s = Node('s')
    t = Node('t')
    x = Node('x')
    y = Node('y')
    z = Node('z')

    r.indegree = 0
    r.adjacency_list.extend([(t, 3), (s, -1)])
    s.indegree = 1
    s.adjacency_list.extend([(t, 2), (x, 6)])
    t.indegree = 2
    t.adjacency_list.extend([(x, 7), (y, 4)])
    x.indegree = 2
    x.adjacency_list.extend([(y, 5), (z, 1)])
    y.indegree = 2
    y.adjacency_list.extend([(z, -2)])
    z.indegree = 2
    z.adjacency_list.extend([])

    nodes = [r, s, t, x, y, z]
    shortest_path_dag = ShortestPathDAG(nodes)
    shortest_path_dag.topological_sort()

    # r s t x y z 
    for node in shortest_path_dag.topological_sorted_list:
        print(node.name, end=' ')

DAGの最短経路

トポロジカルソート後の最短経路の計算は簡単に行えます。

開始地点の最短距離を0、その他を無限大に設定し、トポロジカルソート順に最短距離の更新を行うだけです。

計算量は\(O(V+E)\)です。

有向非巡回グラフ: 深さ優先探索

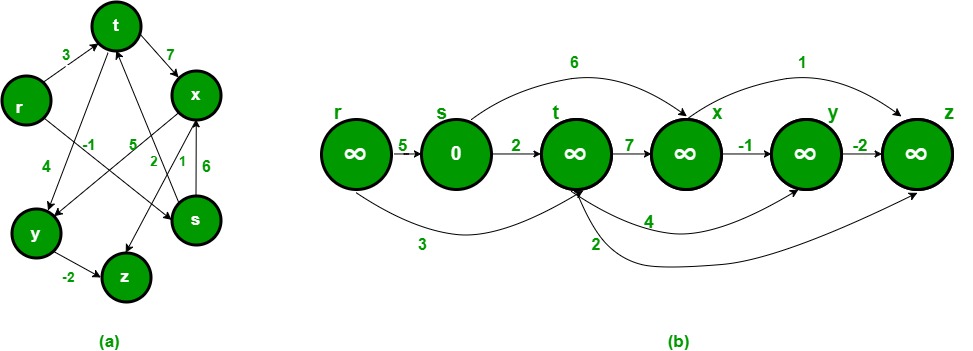
以下のグラフ(b) を探索します。

import collections
import sys


class Node(object):

    def __init__(self, name):
        self.name = name
        self.indegree = 0
        self.adjacency_list = []
        self.min_distance = sys.maxsize
        self.predecessor = None
        

class ShortestPathDAG(object):

    def __init__(self, start_node, nodes):
        self.start_node = start_node
        self.nodes = nodes
        self.topological_sorted_list = []

    def _topological_sort(self):

        queue = collections.deque()

        for node in self.nodes:
            if node.indegree == 0:
                queue.append(node)

        while queue:
            current_node = queue.popleft()
            self.topological_sorted_list.append(current_node)
            for neighbor, _ in current_node.adjacency_list:
                neighbor.indegree -= 1
                if neighbor.indegree == 0:
                    queue.append(neighbor)

        if len(self.nodes) != len(self.topological_sorted_list):
            raise Exception('Not DAG')

    def calculate_shoretest_path(self):
        self._topological_sort()
        self.start_node.min_distance = 0

        for node in self.topological_sorted_list:
            for neighbor, weight in node.adjacency_list:
                temp_distance = node.min_distance + weight
                if temp_distance < neighbor.min_distance:
                    neighbor.min_distance = temp_distance
                    neighbor.predecessor = node
                    
    def show_shotest_path(self, goal):
        current_node = goal
        order_list = []
        while current_node is not None:
            order_list.append(current_node.name)
            current_node = current_node.predecessor
        print(f'from {self.start_node.name} to {goal.name} distance {goal.min_distance}', order_list[::-1])


if __name__ == '__main__':
    r = Node('r')
    s = Node('s')
    t = Node('t')
    x = Node('x')
    y = Node('y')
    z = Node('z')

    r.indegree = 0
    r.adjacency_list.extend([(s, 5), (t, 3)])
    s.indegree = 1
    s.adjacency_list.extend([(t, 2), (x, 6)])
    t.indegree = 2
    t.adjacency_list.extend([(x, 7), (y, 4), (z, 2)])
    x.indegree = 2
    x.adjacency_list.extend([(y, -1), (z, 1)])
    y.indegree = 2
    y.adjacency_list.extend([(z, -2)])
    z.indegree = 3
    z.adjacency_list.extend([])

    nodes = [r, s, t, x, y, z]
    shortest_path_dag = ShortestPathDAG(s, nodes)
    shortest_path_dag.calculate_shoretest_path()
    # from s to r distance 9223372036854775807 ['r']
    shortest_path_dag.show_shotest_path(r)
    # from s to s distance 0 ['s']
    shortest_path_dag.show_shotest_path(s)
    # from s to t distance 2 ['s', 't']
    shortest_path_dag.show_shotest_path(t)
    # from s to x distance 6 ['s', 'x']
    shortest_path_dag.show_shotest_path(x)
    # from s to y distance 5 ['s', 'x', 'y']
    shortest_path_dag.show_shotest_path(y)
    # from s to z distance 3 ['s', 'x', 'y', 'z']
    shortest_path_dag.show_shotest_path(z)

想定通りの結果になりました。

最長経路問題

最長経路問題はNP完全問題です。

最短経路とは逆の問題で、最長単純道問題もある。最短経路の場合は、最短経路の部分問題もやはり最短経路であるが、最長単純道の場合、部分構造最適性が成立しておらず、貪欲法などで解くことが出来ない。辺の重みなしであっても、NP完全問題である。
出典: フリー百科事典『ウィキペディア（Wikipedia）』

しかし、DAGであればトポロジカルソートを使う最短経路とほぼ同様な考え方で解くことができます。

Longest Path in a Directed Acyclic Graph