[Python] 資本資産価格モデル CAPM

2020/3/23 プログラミング, 経済学/数学

Python で資本資産価格モデルを実装します。

資本資産価格モデル CAPM
資本資産価格モデル（しほんしさんかかくモデル、英:Capital Asset Pricing Model,CAPM、シーエーピーエム、キャップエム）とは、金融資産の期待収益率のクロスセクション構造を記述するモデル。 出典: フリー百科事典『ウィキペディア（Wikipe...
yottagin.com
2020-03-21 16:20

個別資産として バークシャーハサウェイ（BRK-A）、マーケット全体として S&P500 index （ ^GSPC ）を使います。

無リスク資産の収益率は 2% で固定し簡略化します。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

情報の取得と月次リターン

情報の取得

yahoo finance から日次の調整終値を取得します。

以下と同じです。

[Python] 現代ポートフォリオ理論
Python で現代ポートフォリオ理論に基づいた最適な資産配分を計算します。 バークシャーハサウェイの2020年2月ポートフォリオ上位6銘柄を使います。 バークシャーハサウェイ（BRK）の最新ポートフォリオ　銀行株売られる クラ...
yottagin.com
2020-03-19 15:04
import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    print(data.head())
    print(data.tail())

月次リターンの計算

日次の調整終値から月次リターンを計算します。

まずは、pandas の resample を使い、日次調整終値から月次の平均調整終値を計算します。

pandasで時系列データをリサンプリングするresample, asfreq

その後、対数収益率を計算します。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_monthly_returns(data):
    data = data.resample('M').mean()
    returns = np.log(data/data.shift(1))
    # drop NAN for np.polyfit
    returns.dropna(inplace=True)
    return returns


if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(data.head())
    # print(data.tail())
    
    returns = calc_monthly_returns(data)
    print(returns.head())
    print(returns.tail())
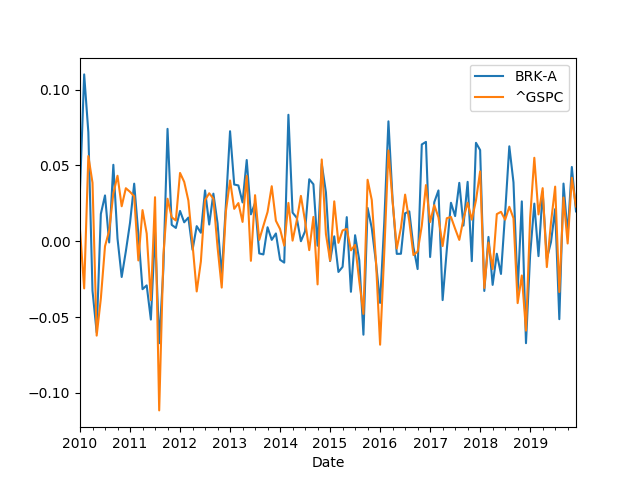
    returns.plot()
    plt.show()
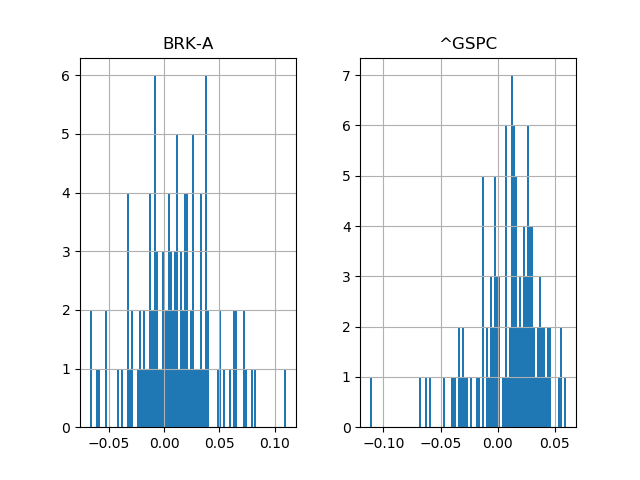
    returns.hist(bins=100)
    plt.show()
月次対数収益率の時系列データ
月次対数収益率のヒストグラム

CAPMの公式による\(\beta\)の計算

以下の公式に従い\(\beta\)を計算します。

$$ {\beta}_i = \frac{Cov(R_i, R_m)}{Var(R_m)} $$

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_monthly_returns(data):
    data = data.resample('M').mean()
    returns = np.log(data/data.shift(1))
    # drop NAN for np.polyfit
    returns.dropna(inplace=True)
    return returns

def calc_beta(returns):
    cov_matrix = np.array(returns.cov())
    print(cov_matrix)
    beta = cov_matrix[0, 1] / cov_matrix[1, 1]
    return beta

if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(data.head())
    # print(data.tail())
    
    returns = calc_monthly_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # returns.plot()
    # plt.show()
    # returns.hist(bins=100)
    # plt.show()

    beta = calc_beta(returns)
    print('Beta', beta)

[[0.00107756 0.00054425]
 [0.00054425 0.00076873]]
Beta 0.7079843244326955

回帰による\(\beta\)と\(\alpha\)の計算

回帰分析で\(\beta\)と\(\alpha\)を求めます。

回帰分析には、numpy の polyfit を使います。

numpy.polyfit

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_monthly_returns(data):
    data = data.resample('M').mean()
    returns = np.log(data/data.shift(1))
    # drop NAN for np.polyfit
    returns.dropna(inplace=True)
    return returns

def calc_beta(returns):
    cov_matrix = np.array(returns.cov())
    # print(cov_matrix)
    beta = cov_matrix[0, 1] / cov_matrix[1, 1]
    return beta

def regression_beta_alpha(returns):
    beta, alpha = np.polyfit((np.array(returns.iloc[:, 1])-RISK_FREE_RATE), 
                             (np.array(returns.iloc[:, 0])-RISK_FREE_RATE) , deg=1)
    return beta, alpha

if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(data.head())
    # print(data.tail())
    
    returns = calc_monthly_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # returns.plot()
    # plt.show()
    # returns.hist(bins=100)
    # plt.show()

    beta = calc_beta(returns)
    print('Beta', beta)

    beta_reg, alpha_reg = regression_beta_alpha(returns)
    print('Beta from Reg:',beta_reg, 'Alpha:', alpha_reg)

  

Beta 0.7079843244326955
Beta from Reg: 0.7079843244326959 Alpha: -0.0018562495855438549

\(\beta\)は、公式に従う場合、回帰分析で求めた場合、当然ですが、ともにほぼ同じ値となっています。

また、 \(\alpha\) が負になっており、無リスク資産の収益率が2%であると仮定した場合、バークシャーハサウェイは CAPM では割高になっていると考えられます。

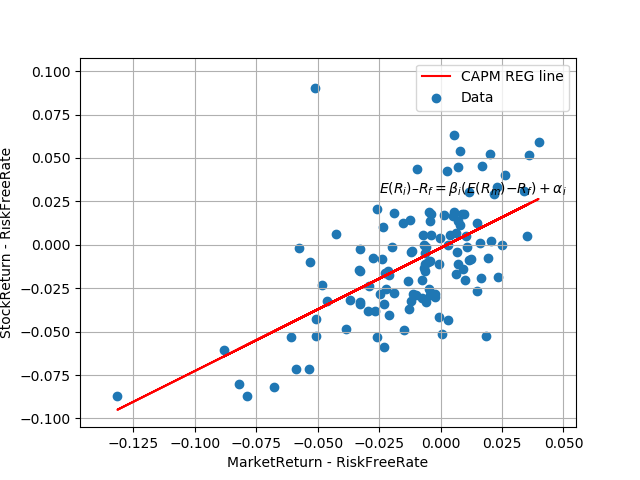
期待収益率の計算と図示

CAPMの下での期待収益率を計算し、またモデルを図示します。

import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize

from pandas_datareader import data as pdr
import yfinance as yf
import requests_cache
# override pandas_datareader
yf.pdr_override()

# casche for downloaded data
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='cache', backend='sqlite', expire_after=expire_after)

# '^GSPC' is S&P 500 index ticker
STOCKS = ['BRK-A', '^GSPC']
START = pd.to_datetime('2010-01-01') 
END = pd.to_datetime('2020-01-01')

RISK_FREE_RATE = 0.02

def download_data_adjclose(stocks):
    data =  pdr.get_data_yahoo(stocks, start=START, end=END)['Adj Close']
    return data

def calc_monthly_returns(data):
    data = data.resample('M').mean()
    returns = np.log(data/data.shift(1))
    # drop NAN for np.polyfit
    returns.dropna(inplace=True)
    return returns

def calc_beta(returns):
    cov_matrix = np.array(returns.cov())
    # print(cov_matrix)
    beta = cov_matrix[0, 1] / cov_matrix[1, 1]
    return beta

def regression_beta_alpha(returns):
    beta, alpha = np.polyfit((np.array(returns.iloc[:, 1])-RISK_FREE_RATE), 
                             (np.array(returns.iloc[:, 0])-RISK_FREE_RATE) , deg=1)
    return beta, alpha

if __name__ == '__main__':
    data = download_data_adjclose(STOCKS)
    # print(data.head())
    # print(data.tail())
    
    returns = calc_monthly_returns(data)
    # print(returns.head())
    # print(returns.tail())
    # returns.plot()
    # plt.show()
    # returns.hist(bins=100)
    # plt.show()

    beta = calc_beta(returns)
    print('Beta', beta)

    beta_reg, alpha_reg = regression_beta_alpha(returns)
    print('Beta from Reg:',beta_reg, 'Alpha:', alpha_reg)

    expected_return = RISK_FREE_RATE + \
        beta*(returns.iloc[:, 1].mean()*12-RISK_FREE_RATE)
    print('Expected Return', expected_return)

    # plot results
    fig, axis = plt.subplots(1)
    axis.scatter(returns.iloc[:, 1]-RISK_FREE_RATE, 
                 returns.iloc[:, 0]-RISK_FREE_RATE, label='Data')
    axis.plot(returns.iloc[:, 1]-RISK_FREE_RATE,
              beta_reg*(returns.iloc[:, 1]-RISK_FREE_RATE)+alpha_reg, 
              color='red', label='CAPM REG line')
    plt.legend()
    plt.grid(True)
    plt.xlabel('MarketReturn - RiskFreeRate')
    plt.ylabel('StockReturn - RiskFreeRate')
    plt.text(-0.025, 0.03, r'$E(R_i) – R_f = {\beta}_i (E(R_m)−R_f) + {\alpha}_i $')
    plt.show()
    


Beta 0.7079843244326955
Beta from Reg: 0.7079843244326959 Alpha: -0.0018562495855438549
Expected Return 0.07996021496399774

CAPM