Python でウィーナー過程のシミュレーションを行います。
数学におけるウィーナー過程(ウィーナーかてい、英: Wiener process)は、ノーバート・ウィーナーの名にちなんだ連続時間確率過程である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ウィーナー過程\(W_t\)は、以下の3つの条件により特徴づけられます。
- \(W_0 = 0\)
- \(W_t\) はほとんど確実に(確率 1 で)連続である。
- \(W_t\)は独立増分を持ち、\(0 \leq s \le t \)なる任意の\( s, t \)に対して、 \(W_t-W_s\)は正規分布\(N(0, t-s)\)に従う。
numpy.random.normal で独立増分を生成し、 numpy.cumsum で生成した独立増分を足し合わせるだけです。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
def winer_process(dt, x0=0, n=1000):
t = np.linspace(0, n, n+1)
w = np.zeros(n+1)
w[1:n+1] = np.cumsum(np.random.normal(0, dt, n))
return t, w
def plot_brownian_motion(dt, x0=0, n=1000):
t, w = winer_process(dt, x0, n)
plt.plot(t, w)
plt.xlabel('Time(t)')
plt.ylabel('W(t)')
plt.title(f'Brownian Motion when dt={dt}')
plt.show()
if __name__ == '__main__':
plot_brownian_motion(dt=0, x0=0, n=1000)
plot_brownian_motion(dt=0.1, x0=0, n=1000)
plot_brownian_motion(dt=100, x0=0, n=1000)
このコードでは、以下のようなブラウン運動が生成されました。
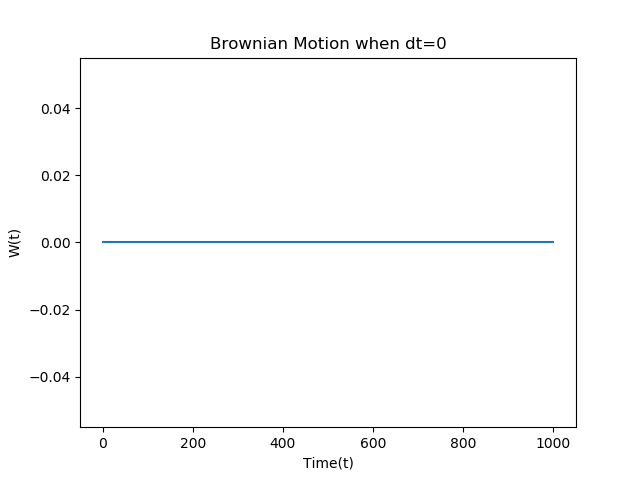
独立増分\(dt=0\)の時は当然ながら全く動きがありません。
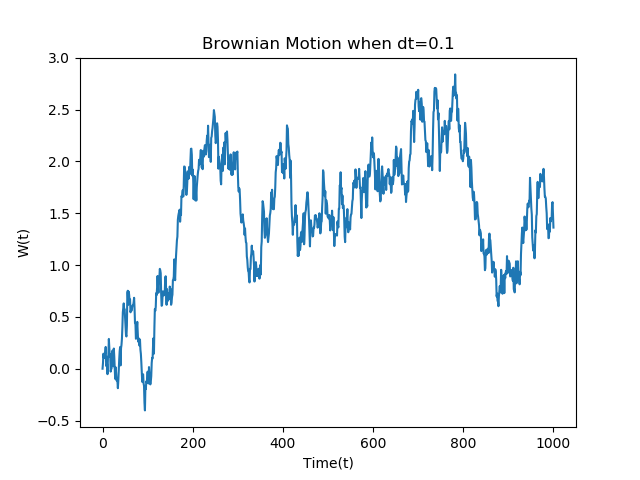
独立増分\(dt=0.1\)では以下のようにランダムな動きがでます。
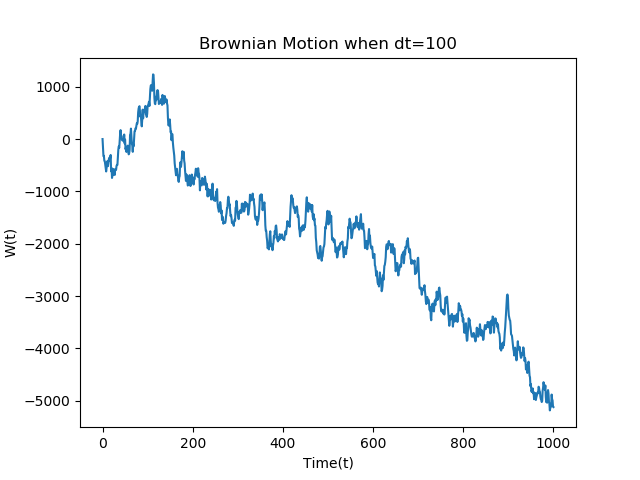
独立増分\(dt=100\)では、変動が \(dt=0.1\) と比較してかなり大きくなります。