scikit-learn という有名なモジュールを用いて、有名なあやめの分類問題を、k近傍法で解いてみます。
IPython で行います。
k近傍法
k近傍法(ケイきんぼうほう、英: k-nearest neighbor algorithm, k-NN)は、特徴空間における最も近い訓練例に基づいた分類の手法であり、パターン認識でよく使われる。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
Wikipedia では何となく難しそうに見えますが、非常に単純なアルゴリズムです。
下は wikipedia の図です。
緑の〇が、青の■、赤の▲、どちらにカテゴリーに属するかを考えます。
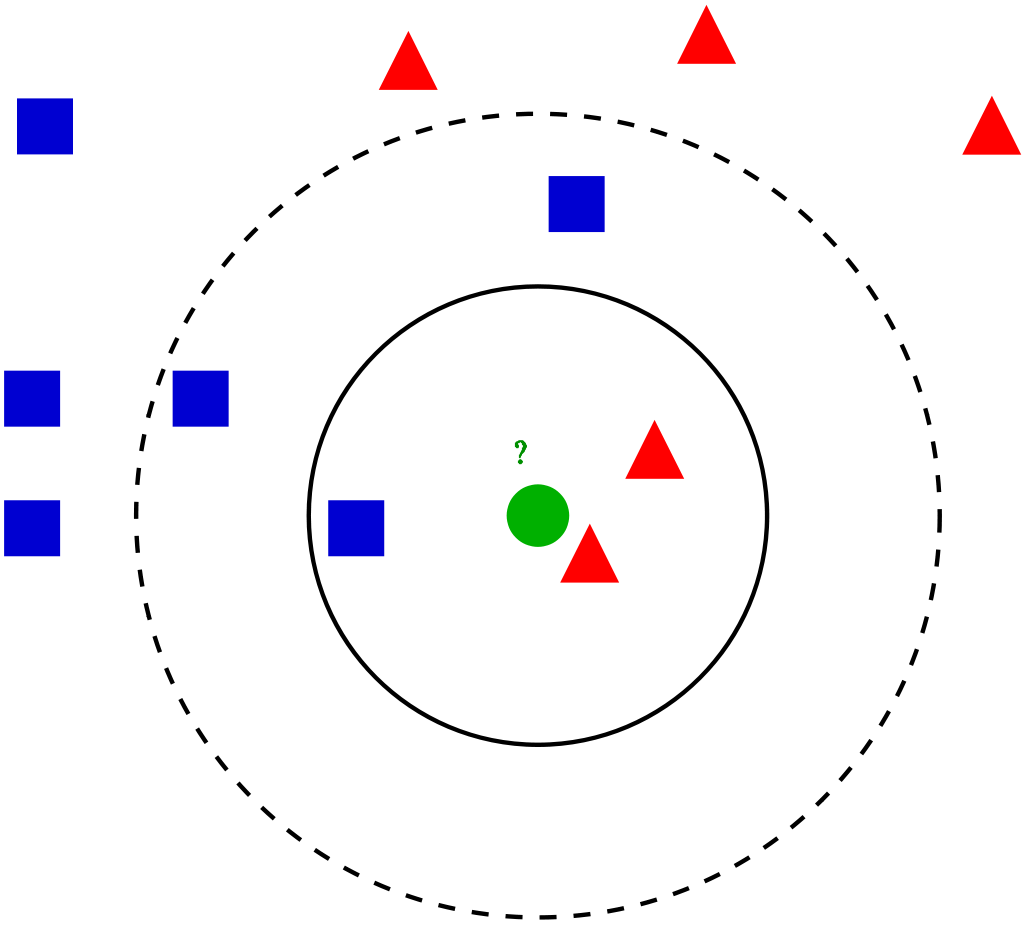
k=1 の場合、1番近いものと同じカテゴリーに分類されるので、緑●は赤▲と同じグループです。
k=3 であれば、1番目、2番目、3番得目に近いものを使い、例えば、赤▲が2つで青■は1つだから、緑●は赤▲と同じグループと判断します。
k=5である場合、例えば赤▲2つで青■3つだから、緑●は青■と同じグループと判断します。赤2つ▲の方が距離が近いのに青■グループとは納得がいかない!というような場合は、例えば評価の際に距離で重みを付けることで、この場合も赤▲グループに含めるような判断をするアルゴリズムにすることも可能です。
あやめのデータセット
分類問題の例題としてとても有名なデータセットです。
The Iris flower data set or Fisher’s Iris data set is a multivariatedata set introduced by the British statistician and biologistRonald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis.[1]
あやめの花のデータセット、またはフィッシャーのあやめのデータセットとは、英国の統計学者および生物学者のロナルド・フィッシャーが1936年に発表した論文「線形判別分析の一例としての分類問題における多重測定の使用」で用いた、多変量のデータセットのことです。
From Wikipedia, the free encyclopedia
‘sepal’ 「がく片」の縦の長さと横の長さ、’petal’ 「花弁」の縦の長さと横の長さの4つの変数を用いて、その花のあやめはどの種類かを予想してみます。
scikit-learn
Python のオープンソースの機械学習ライブラリです。
あやめの分類問題を解く
データセットの読み込み
scikit-learn にデータセットが用意されているので、読み込みます。
In [1]: from sklearn.datasets import load_iris In [2]: iris = load_iris()
読み込んだデータセットをデータフレームに変換し、基本統計量を確認します。
In [4]: import pandas as pd
In [5]: df = pd.DataFrame(iris.data, columns=iris.feature_names)
In [6]: df.describe()
Out[6]:
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
count 150.000000 150.000000 150.000000 150.000000
mean 5.843333 3.057333 3.758000 1.199333
std 0.828066 0.435866 1.765298 0.762238
min 4.300000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.300000
50% 5.800000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000
データの可視化
以下を参考に散布図行列を作成します。
Python, pandas, seabornでペアプロット図(散布図行列)を作成
In [7]: import seaborn as sns In [8]: import numpy as np In [9]: df['species'] = np.array([iris.target_names[i] for i in iris.target]) In [10]: sns.pairplot(df, hue='species');
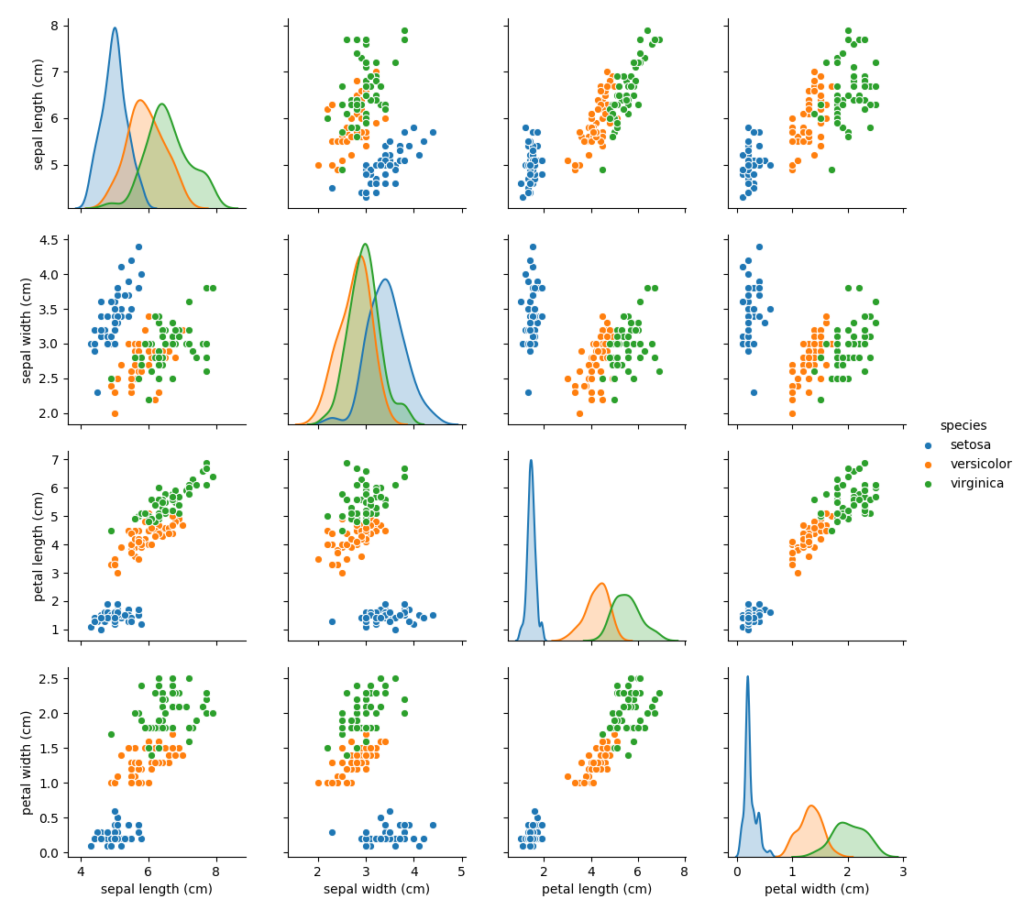
何となくきれいに分かれているので、これらのデータを用いることでうまく分類ができるように思われます。
訓練データとテストデータの分割
scikit-learn に含まれる関数を用いて、訓練用とテスト用のデータに分割します。
sklearn.model_selection.train_test_split
In [12]: from sklearn.model_selection import train_test_split
...: X_train, X_test, y_train, y_test = train_test_split(df[iris.feature_names],
...: iris.target,
...: test_size=0.5,
...: stratify=iris.target,
...: random_state=0)
test_size は、訓練用データとテスト用データの分割の比率を決めます。
stratify は、分割後のそれぞれの割合が、目標のそれぞれの割合と同じになるように分割します。
random_state は、0で乱数を固定しています。
学習
scikit-learn に含まれる関数を用いて、 k近傍法のモデルによる学習を行います。
sklearn.neighbors.KNeighborsClassifier
色々と設定できますが、ここでは、k の数のみ、3、5、 7 と変えて学習を行ってみます。k のデフォルトは5だそうです。
In [14]: from sklearn.neighbors import KNeighborsClassifier
...: knn_3 = KNeighborsClassifier(n_neighbors=3)
...: knn_3.fit(X_train, y_train)
Out[14]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=3, p=2,
weights='uniform')
In [15]: knn_5 = KNeighborsClassifier(n_neighbors=5)
...: knn_5.fit(X_train, y_train)
Out[15]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
In [16]: knn_7 = KNeighborsClassifier(n_neighbors=5)
...: knn_7.fit(X_train, y_train)
Out[16]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
予測とその評価
正解率 accuracy のスコアを確認します。
In [9]: knn_3.score(X_test, y_test) Out[9]: 0.9733333333333334 In [10]: knn_5.score(X_test, y_test) Out[10]: 0.96 In [11]: knn_7.score(X_test, y_test) Out[11]: 0.96
デフォルトの k=5 を用いて、Confusion matrix を作成します。
sklearn.metrics.confusion_matrix
In [16]: predicted = knn_5.predict(X_test)
...: from sklearn.metrics import confusion_matrix
...: confusion_matrix = pd.DataFrame(confusion_matrix(y_test, predicted),
...: columns=iris.target_names,
...: index=iris.target_names)
...: confusion_matrix
Out[16]:
setosa versicolor virginica
setosa 25 0 0
versicolor 0 23 2
virginica 0 1 24
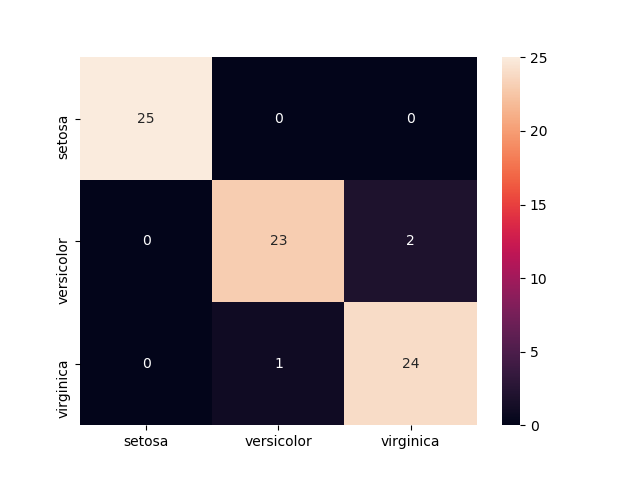
Confusion matrix を、sea born のヒートマップでかっこよく表現してみます。
In [18]: sns.heatmap(confusion_matrix, annot=True);