[Python] クラスカル法

クラスカル法を用いて、重み付き無向グラフの最小全域木を求めます。

以下の記事の続きです。

プリム法は、ある頂点を選び、その頂点と繋がる辺の中で最小のものを選ぶことで、結果的に最小全域木を得ることができるアルゴリズムです。

クラスカル法は、閉路を作らないように最小の辺を選んでいくことで、最終的に最小全域木を得ることができるアルゴリズムです。

プリム法もクラスカル法も貪欲法ですが、数学的に最小全域木を得ると証明されています。

閉路を作らないようにするために、素集合データ集合を使います。

クラスカル法

クラスカル法（英: Kruskal’s algorithm）は、グラフ理論において重み付き連結グラフの最小全域木を求める最適化問題のアルゴリズムである。
出典: フリー百科事典『ウィキペディア（Wikipedia）』

以下のようなアルゴリズムになります。

グラフ内の各頂点を個別の木とする森F（素集合データ構造）を作成
グラフ内のすべての辺を含む集合Sを作成
Sは空ではなく、Fは全域木ではない時
- Sから最小の重みを持つ辺を削除
- 削除された辺が2つの異なる木を接続する場合、森Fに追加し、2つの木を1つの木に結合（素集合データ構造の Union & Find を用いる）
アルゴリズムの終了時、森はグラフの最小領域木となる

プリム法の時と同じ以下のグラフの探索を行います。

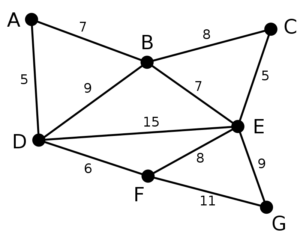
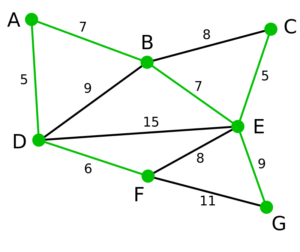
探索の結果、以下の緑線の最小全域木が求まり、重さの総和は39になります。

import heapq
import sys

class Vertex(object):
    def __init__(self, id):
        self.id = id
        self.adjacent = {}
        self.distance = sys.maxsize
        self.visited = False
        self.previous = None
    
    def __lt__(self, other):
        return self.distance < other.distance

    def add_neighbor(self, neighbor, weight=0):
        self.adjacent[neighbor] = weight
    
    def get_neighbors(self):
        return self.adjacent

    def get_connections(self):
        return self.adjacent.keys()  

    def get_vertex_id(self):
        return self.id

    def get_weight(self, neighbor):
        return self.adjacent[neighbor]
    
    def set_distance(self, distance):
        self.distance = distance

    def get_distance(self):
        return self.distance

    def set_previous(self, previous_vertex):
        self.previous = previous_vertex 
    
    def get_previous(self):
        return self.previous
    
    def set_visited(self):
        self.visited= True


class Graph(object):
    def __init__(self):
        self.vertex_dict = {}
        self.num_vertex = 0
    
    def __iter__(self):
        return iter(self.vertex_dict.values())

    def __len__(self):
        return self.num_vertex

    def add_vertex(self, id):
        self.num_vertex = self.num_vertex + 1
        new_vertex = Vertex(id)
        self.vertex_dict[id] = new_vertex
        return new_vertex

    def get_vertex(self, id):
        if id in self.vertex_dict:
            return self.vertex_dict[id]
        else:
            return None

    def add_edge(self, frm, to, weight=0):
        if frm not in self.vertex_dict:
            self.add_vertex(frm)
        if to not in self.vertex_dict:
            self.add_vertex(to)
        self.vertex_dict[frm].add_neighbor(self.vertex_dict[to], weight)
        self.vertex_dict[to].add_neighbor(self.vertex_dict[frm], weight)

    def get_vertices(self):
        return self.vertex_dict.keys()

    def get_edges(self):
        edges = []
        for v in self.vertex_dict.values():
            for w in v.get_connections():
                vid = v.get_vertex_id()
                wid = w.get_vertex_id()
                edges.append((vid, wid, v.get_weight(w)))
        return edges


def prim(graph, source):
    source.set_distance(0)

    priority_queue = [(vertex.get_distance(), vertex) for vertex in graph]
    heapq.heapify(priority_queue)

    while len(priority_queue):
        nearest_vrtex = heapq.heappop(priority_queue)
        current = nearest_vrtex[1]
        current.set_visited()

        for next in current.adjacent:
            if next.visited:
                continue
            new_distance = current.get_weight(next)

            if next.get_distance() > new_distance:
                next.set_distance(new_distance)
                next.set_previous(current)
        
        heapq.heapify(priority_queue)
    
    print('プリム法')
    total_distance = 0
    for vertex in graph.vertex_dict.values():
        if vertex.get_previous():
            print(f'辺 {vertex.get_vertex_id()}{vertex.previous.get_vertex_id()} --> {vertex.get_distance()}')
            total_distance += vertex.get_distance()
    print(f'総距離 {total_distance}')

# 素集合データ構造
parent = dict()
rank = dict()

def make_disjoint_set(vertex):
    parent[vertex] = vertex
    rank[vertex] = 0

def find(vertex):
    if parent[vertex] != vertex:
        parent[vertex] = find(parent[vertex])
    return parent[vertex]

def union(vertex1, vertex2):
    root1 = find(vertex1)
    root2 = find(vertex2)
    if root1 != root2:
        if rank[root1] > rank[root2]:
            parent[root2] = root1
        else:
            parent[root1] = root2
            if rank[root1] == rank[root2]: 
                rank[root2] += 1


def kruskal(graph):
    edges = []
    for vertex in graph:
        disjoint_set = make_disjoint_set(vertex)
        for neighbor in vertex.get_connections():
            edges.append((vertex.get_weight(neighbor), vertex, neighbor))

    edges.sort()
    # 最小全域木は、リストに保存して出力を簡略化。
    minimum_spanning_tree = []
    for edge in edges:
        weight, vertex1, vertex2 = edge
        if find(vertex1) != find(vertex2):
            union(vertex1, vertex2)
            minimum_spanning_tree.append((weight, vertex1.get_vertex_id(), vertex2.get_vertex_id()))
    
    print('クルスカル法')
    distance = 0
    for weight, vertex1, vertex2 in minimum_spanning_tree:
        print(f'辺 {vertex1}{vertex2} --> {weight}')
        distance += weight
    print(f'総距離 {distance}')


if __name__ == '__main__':

    graph = Graph()
    graph.add_vertex('a')
    graph.add_vertex('b')
    graph.add_vertex('c')
    graph.add_vertex('d')
    graph.add_vertex('e')
    graph.add_vertex('f')
    graph.add_vertex('g')
    graph.add_edge('a', 'b', 7)  
    graph.add_edge('a', 'd', 5)
    graph.add_edge('b', 'c', 8)
    graph.add_edge('b', 'd', 9)
    graph.add_edge('b', 'e', 7)
    graph.add_edge('c', 'e', 5)
    graph.add_edge('d', 'e', 15)
    graph.add_edge('d', 'f', 6)
    graph.add_edge('e', 'f', 8)
    graph.add_edge('e', 'g', 9)
    graph.add_edge('f', 'g', 11)

    source = graph.get_vertex('d')
    prim(graph, source)
    # プリム法
    # 辺 ad --> 5
    # 辺 ba --> 7
    # 辺 ce --> 5
    # 辺 eb --> 7
    # 辺 fd --> 6
    # 辺 ge --> 9
    # 総距離 39

    kruskal(graph)
    # クルスカル法
    # 辺 da --> 5
    # 辺 ce --> 5
    # 辺 df --> 6
    # 辺 ab --> 7
    # 辺 be --> 7
    # 辺 eg --> 9
    # 総距離 39

想定通りの結果を得ることができました。